题目内容
(本题满分14分)已知椭圆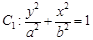
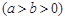 的右顶点
的右顶点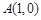 ,过
,过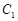 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为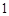 .
.
(I) 求椭圆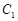 的方程;
的方程;
(II) 设点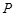 在抛物线
在抛物线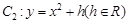 上,
上,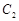 在点
在点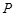 处的切线与
处的切线与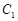 交于点
交于点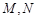 .当线段
.当线段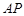 的中点与
的中点与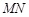 的中点的横坐标相等时,求
的中点的横坐标相等时,求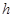 的最小值.
的最小值.
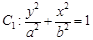
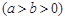 的右顶点
的右顶点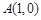 ,过
,过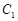 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为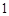 .
.(I) 求椭圆
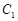 的方程;
的方程;(II) 设点
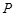 在抛物线
在抛物线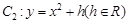 上,
上,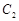 在点
在点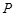 处的切线与
处的切线与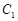 交于点
交于点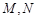 .当线段
.当线段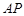 的中点与
的中点与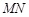 的中点的横坐标相等时,求
的中点的横坐标相等时,求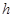 的最小值.
的最小值.(I)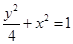 ;(II)
;(II)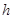 的最小值为1.
的最小值为1.
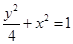 ;(II)
;(II)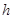 的最小值为1.
的最小值为1.本试题主要是考查了椭圆的方程的求解以及直线与椭圆的位置关系的运用。
(1)因为椭圆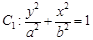
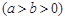 的右顶点
的右顶点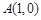 ,过
,过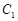 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为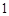 .,根据性质得到椭圆的方程。
.,根据性质得到椭圆的方程。
(2)不妨设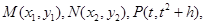 则抛物线
则抛物线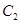 在点P处的切线斜率为
在点P处的切线斜率为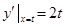 ,直线MN的方程为
,直线MN的方程为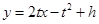 ,将上式代入椭圆
,将上式代入椭圆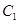 的方程中,得
的方程中,得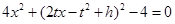 ,即
,即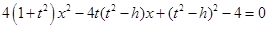
结合判别式得到范围和最值。
解:(I)由题意得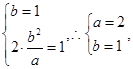 所求的椭圆方程为
所求的椭圆方程为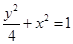 ,
,
(II)不妨设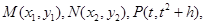 则抛物线
则抛物线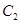 在点P处的切线斜率为
在点P处的切线斜率为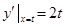 ,直线MN的方程为
,直线MN的方程为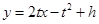 ,将上式代入椭圆
,将上式代入椭圆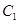 的方程中,得
的方程中,得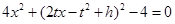 ,即
,即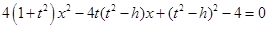 ,因为直线MN与椭圆
,因为直线MN与椭圆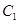 有两个不同的交点,所以有
有两个不同的交点,所以有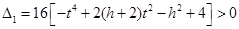 ,
,
设线段MN的中点的横坐标是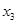 ,则
,则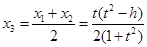 ,
,
设线段PA的中点的横坐标是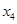 ,则
,则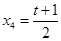 ,由题意得
,由题意得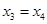 ,即有
,即有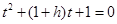 ,其中的
,其中的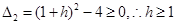 或
或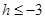 ;
;
当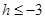 时有
时有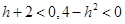 ,因此不等式
,因此不等式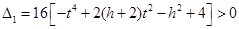 不成立;因此
不成立;因此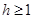 ,当
,当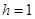 时代入方程
时代入方程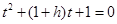 得
得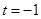 ,将
,将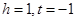 代入不等式
代入不等式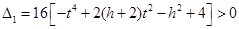 成立,因此
成立,因此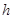 的最小值为1.
的最小值为1.
(1)因为椭圆
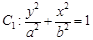
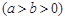 的右顶点
的右顶点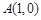 ,过
,过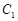 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为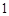 .,根据性质得到椭圆的方程。
.,根据性质得到椭圆的方程。(2)不妨设
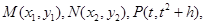 则抛物线
则抛物线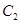 在点P处的切线斜率为
在点P处的切线斜率为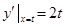 ,直线MN的方程为
,直线MN的方程为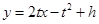 ,将上式代入椭圆
,将上式代入椭圆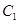 的方程中,得
的方程中,得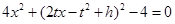 ,即
,即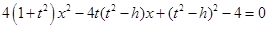
结合判别式得到范围和最值。
解:(I)由题意得
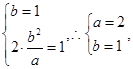 所求的椭圆方程为
所求的椭圆方程为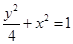 ,
,(II)不妨设
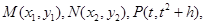 则抛物线
则抛物线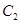 在点P处的切线斜率为
在点P处的切线斜率为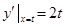 ,直线MN的方程为
,直线MN的方程为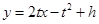 ,将上式代入椭圆
,将上式代入椭圆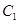 的方程中,得
的方程中,得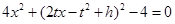 ,即
,即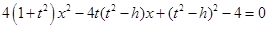 ,因为直线MN与椭圆
,因为直线MN与椭圆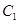 有两个不同的交点,所以有
有两个不同的交点,所以有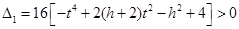 ,
,设线段MN的中点的横坐标是
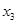 ,则
,则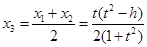 ,
,设线段PA的中点的横坐标是
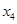 ,则
,则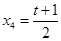 ,由题意得
,由题意得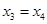 ,即有
,即有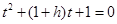 ,其中的
,其中的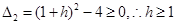 或
或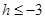 ;
;当
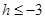 时有
时有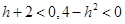 ,因此不等式
,因此不等式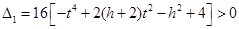 不成立;因此
不成立;因此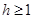 ,当
,当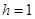 时代入方程
时代入方程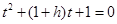 得
得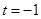 ,将
,将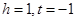 代入不等式
代入不等式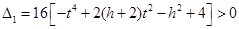 成立,因此
成立,因此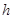 的最小值为1.
的最小值为1.
练习册系列答案
相关题目
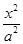 +
+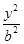 =1(a>b>0)的左右顶点为
=1(a>b>0)的左右顶点为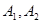 ,上下顶点为
,上下顶点为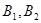 , 左右焦点为
, 左右焦点为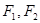 ,若
,若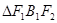 为等腰直角三角形(1)求椭圆的离心率(2)若
为等腰直角三角形(1)求椭圆的离心率(2)若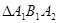 的面积为6
的面积为6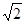 ,求椭圆的方程
,求椭圆的方程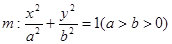 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为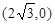 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且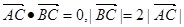
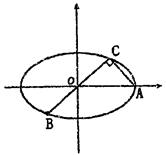
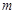 的方程;
的方程;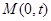 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,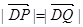 ,求实数t的取值范围.
,求实数t的取值范围.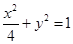 上,则
上,则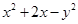 的最大值为
的最大值为 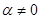 的直线
的直线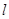 过椭圆
过椭圆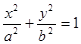
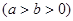 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则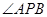 为 ( )
为 ( )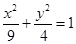 与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.
与坐标轴正半轴的两交点,在第一象限的椭圆弧上求一点P,使四边形OPAB的面积最大.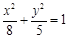 的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.
的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程. 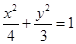 的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当
的左顶点为A1,右焦点为F2,点P为该椭圆上一动点,则当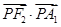 取最小值时,
取最小值时,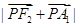 的值为( )
的值为( )


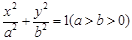 ,过右焦点且不与
,过右焦点且不与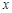 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于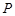 ,
,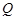 两点,若在椭圆的右准线上存在点
两点,若在椭圆的右准线上存在点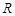 ,使
,使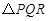 为正三角形,则椭圆的离心率的取值范围是 .
为正三角形,则椭圆的离心率的取值范围是 .