题目内容
设椭圆的方程为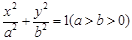 ,过右焦点且不与
,过右焦点且不与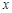 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于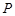 ,
,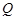 两点,若在椭圆的右准线上存在点
两点,若在椭圆的右准线上存在点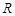 ,使
,使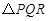 为正三角形,则椭圆的离心率的取值范围是 .
为正三角形,则椭圆的离心率的取值范围是 .
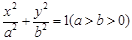 ,过右焦点且不与
,过右焦点且不与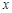 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于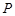 ,
,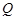 两点,若在椭圆的右准线上存在点
两点,若在椭圆的右准线上存在点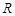 ,使
,使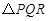 为正三角形,则椭圆的离心率的取值范围是 .
为正三角形,则椭圆的离心率的取值范围是 .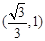
解:设弦PQ的中点为M,过点P、M、Q分别作准线l的垂线,垂足为P'、M'、Q'
则|MM'|=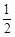 (|PP'|+|QQ'|)=
(|PP'|+|QQ'|)=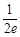 (|PF|+|QF|)=
(|PF|+|QF|)=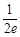 |PQ|
|PQ|
假设存在点R,使△PQR为正三角形,则由|RM|=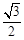 |PQ|,且|MM'|<|RM|
|PQ|,且|MM'|<|RM|
得: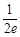 |PQ|<
|PQ|< 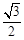 |PQ|
|PQ|
∴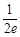 <
<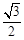 ∴e>
∴e> 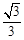
∴椭圆离心率e的取值范围是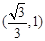
故答案为: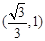
则|MM'|=
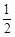 (|PP'|+|QQ'|)=
(|PP'|+|QQ'|)=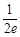 (|PF|+|QF|)=
(|PF|+|QF|)=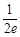 |PQ|
|PQ|假设存在点R,使△PQR为正三角形,则由|RM|=
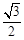 |PQ|,且|MM'|<|RM|
|PQ|,且|MM'|<|RM|得:
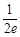 |PQ|<
|PQ|< 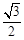 |PQ|
|PQ|∴
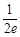 <
<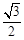 ∴e>
∴e> 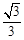
∴椭圆离心率e的取值范围是
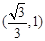
故答案为:
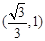

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
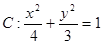 的右顶点是
的右顶点是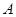 ,上下两个顶点分别为
,上下两个顶点分别为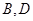 ,四边形
,四边形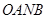 是矩形(
是矩形(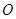 为原点),点
为原点),点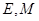 分别为线段
分别为线段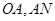 的中点.
的中点.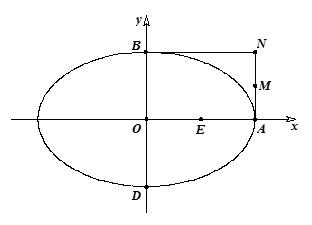
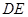 与直线
与直线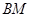 的交点在椭圆
的交点在椭圆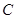 上;
上;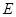 的直线交椭圆于
的直线交椭圆于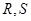 两点,
两点,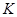 为
为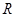 关于
关于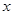 轴的对称点(
轴的对称点(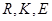 不共线),
不共线),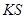 是否经过
是否经过
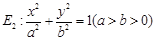 .
.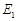 与
与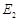 有相同的离心率,过点
有相同的离心率,过点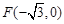 的直线
的直线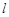 与
与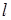 过
过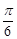 .
.
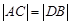 ;
; 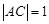 ,求直线
,求直线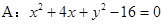 及定点
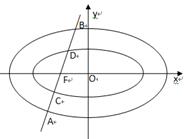
及定点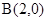 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足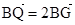 ,
,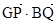 =0.
=0.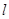 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线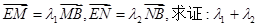 为定值。
为定值。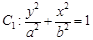
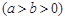 的右顶点
的右顶点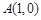 ,过
,过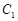 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为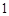 .
.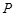 在抛物线
在抛物线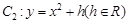 上,
上,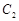 在点
在点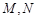 .当线段
.当线段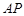 的中点与
的中点与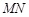 的中点的横坐标相等时,求
的中点的横坐标相等时,求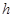 的最小值.
的最小值. 为椭圆
为椭圆 的左、右焦点,若
的左、右焦点,若 为椭圆上一点,且△
为椭圆上一点,且△ 的内切圆的周长等于
的内切圆的周长等于 ,则满足条件的点
,则满足条件的点 ,如果
,如果 的最小值为m,则满足
的最小值为m,则满足 的整点
的整点 的个数为 ( )
的个数为 ( ) 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,则
,则 等于( )
等于( )



 的左右焦点分别为
的左右焦点分别为 ,线段
,线段 被抛物线
被抛物线 的焦点分成5:3两段,则此椭圆的离心率为
的焦点分成5:3两段,则此椭圆的离心率为


