题目内容
7.若函数f(x)=$\sqrt{{2}^{({ax}^{2}+ax+2)}-2}$定义域为R,则a的取值范围是[0,4].分析 根据题意,得出不等式${2}^{{(ax}^{2}+ax+2)}$-2≥0恒成立,再转化为ax2+ax+2≥1恒成立,讨论a的值,求出满足题意的a的取值范围.
解答 解:∵函数f(x)=$\sqrt{{2}^{({ax}^{2}+ax+2)}-2}$的定义域为R,
∴${2}^{{(ax}^{2}+ax+2)}$-2≥0恒成立,
即ax2+ax+2≥1,
即ax2+ax+1≥0;
当a=0时,1≥0;
当a>0时,应有△=a2-4a≤0,
解得0<a≤4;
综上,a的取值范围是[0,4].
故答案为:[0,4].
点评 本题考查了根式与指数函数的图象和性质的应用问题,也考查了不等式的恒成立问题,是基础题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.数列{$\frac{1}{(2n-1)(2n+1)}$}的前n项和为( )
| A. | $\frac{n}{2n+1}$ | B. | $\frac{2n}{2n+1}$ | C. | $\frac{n}{4n+2}$ | D. | $\frac{2n}{n+1}$ |
13.设P(x,y)满足$\left\{\begin{array}{l}{x-2y≥0}\\{x+2y≥0}\end{array}\right.$,且P点到两直线x-2y=0,x+2y=0距离之和不大于$\sqrt{5}$,则x-y的最大值为( )
| A. | $\frac{17}{3}$ | B. | $\frac{15}{4}$ | C. | $\frac{25}{4}$ | D. | $\frac{11}{3}$ |
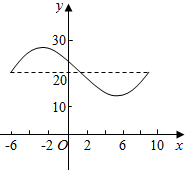 函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.
函数y=Asin(ωx+θ)+b的图象如图所示,则此函数的解析式为y=y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20.