题目内容
已知幂函数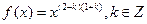 ,且
,且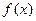 在
在 上单调递增.
上单调递增.
(Ⅰ)求实数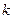 的值,并写出相应的函数
的值,并写出相应的函数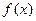 的解析式;
的解析式;
(II)若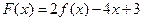 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(III)试判断是否存在正数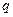 ,使函数
,使函数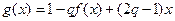 在区间
在区间 上的值域为
上的值域为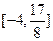 . 若存在,求出
. 若存在,求出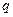 的值;若不存在,请说明理由
的值;若不存在,请说明理由
解:(Ⅰ)由题意知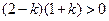 解得
解得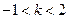
又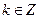 ∴
∴ 或
或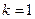 ,分别代入原函数得
,分别代入原函数得 .
.
(II)由已知得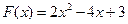 .
.
要使函数不单调,则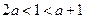 ,则
,则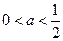 .
.
(III)由已知,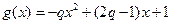
法一:假设存在这样的正数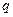 符合题意,则函数
符合题意,则函数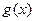 的图象是开口向下的抛物线,其对称轴为
的图象是开口向下的抛物线,其对称轴为
因而,函数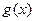 在
在 上的最小值只能在
上的最小值只能在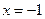 或
或 处取得
处取得
又 ,从而必有
,从而必有
解得
此时, ,其对称轴
,其对称轴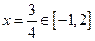
∴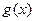 在
在 上的最大值为
上的最大值为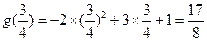 符合题意.
符合题意.
法二: 由(1)知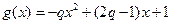 ,假设存在这样的正数
,假设存在这样的正数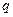 ,符合题意,则函数
,符合题意,则函数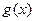
的图象是开口向下的抛物线,其对称轴为 ,
,
(1)当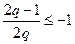 ,且
,且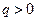 ,即
,即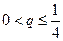 时,
时,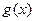 在
在 上单调递减,
上单调递减,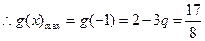 ,则
,则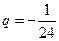 与
与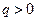 矛盾,故不可能;
矛盾,故不可能;
(2)当 ,且
,且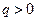 ,即
,即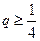 时,有
时,有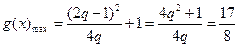
得 或
或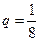 (舍去).
(舍去).
所以  ,此时
,此时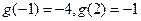 ,
,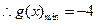 ,符合题意
,符合题意
综上所述,存在正数 ,使函数
,使函数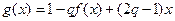 在区间
在区间 上的值域为
上的值域为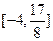
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
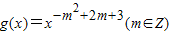 为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.
为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.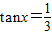 ,求F(x)的值;
,求F(x)的值; 为偶函数,且在区间
为偶函数,且在区间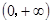 上是单调减函数(Ⅰ)求函数
上是单调减函数(Ⅰ)求函数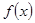 ;(Ⅱ)讨论
;(Ⅱ)讨论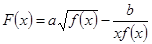 的奇偶性.
的奇偶性.