题目内容
已知函数已知幂函数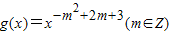 为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.
为偶函数,且在区间(0,+∞)上是单调增函数,又f(x)=sinx+mcosx,F(x)=f′(x)[f(x)+f′(x)]-1,f′(x)是f(x)的导函数.(I)若
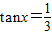 ,求F(x)的值;
,求F(x)的值;(Ⅱ)把F(x)图象的横坐标缩小为原来的一半后得到H(x),求H(x)的单调减区间.
【答案】分析:(I)利用幂函数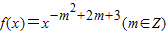 为偶函数,且在区间(0,+∞)上是单调增函数,确定m的值.再求导,即可求得F(x)的值;
为偶函数,且在区间(0,+∞)上是单调增函数,确定m的值.再求导,即可求得F(x)的值;
(Ⅱ)先确定H(x)的解析式,再利用余弦函数的单调性,即可求得H(x)的单调减区间.
解答:解:(I)幂函数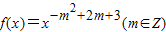 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数
∴-m2+2m+3>0,∴-1<m<3,
又m∈Z,函数f(x)为偶函数,故m=1….(3分)
∴f(x)=sinx+cosx,f'(x)=cosx-sinx
∴F(x)=f′(x)[f(x)+f′(x)]-1=2(cosx-sinx)cosx-1=cos2x-sin2x=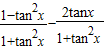
∵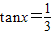 ,F(x)=
,F(x)=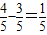 .…(6分)
.…(6分)
(Ⅱ)由(I)知:F(x)=cos2x-sin2x=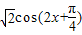 ,∴
,∴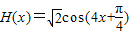 .
.
令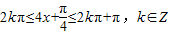 得:
得: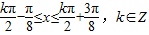
∴H(x)的单调减区间为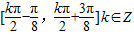 …(12分)
…(12分)
点评:本题考查幂函数,考查导数知识的运用,考查三角函数的化简,考查函数的单调性,考查学生的计算能力,属于中档题.
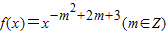 为偶函数,且在区间(0,+∞)上是单调增函数,确定m的值.再求导,即可求得F(x)的值;
为偶函数,且在区间(0,+∞)上是单调增函数,确定m的值.再求导,即可求得F(x)的值;(Ⅱ)先确定H(x)的解析式,再利用余弦函数的单调性,即可求得H(x)的单调减区间.
解答:解:(I)幂函数
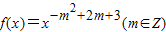 为偶函数,且在区间(0,+∞)上是单调增函数
为偶函数,且在区间(0,+∞)上是单调增函数∴-m2+2m+3>0,∴-1<m<3,
又m∈Z,函数f(x)为偶函数,故m=1….(3分)
∴f(x)=sinx+cosx,f'(x)=cosx-sinx
∴F(x)=f′(x)[f(x)+f′(x)]-1=2(cosx-sinx)cosx-1=cos2x-sin2x=
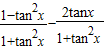
∵
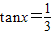 ,F(x)=
,F(x)=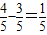 .…(6分)
.…(6分)(Ⅱ)由(I)知:F(x)=cos2x-sin2x=
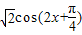 ,∴
,∴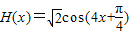 .
.令
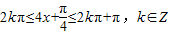 得:
得: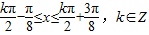
∴H(x)的单调减区间为
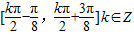 …(12分)
…(12分)点评:本题考查幂函数,考查导数知识的运用,考查三角函数的化简,考查函数的单调性,考查学生的计算能力,属于中档题.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
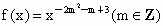 为偶函数,且f(3)<f(5).
为偶函数,且f(3)<f(5).
 在区间[2,3]上为增函数,求实数a的取值集合.
在区间[2,3]上为增函数,求实数a的取值集合.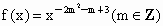 为偶函数,且f(3)<f(5).
为偶函数,且f(3)<f(5).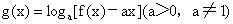 在区间[2,3]上为增函数,求实数a的取值集合.
在区间[2,3]上为增函数,求实数a的取值集合.