题目内容
(本小题满分12分)已知

(1)求函数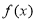 的最小正周期及在区间
的最小正周期及在区间 的最大值;
的最大值;
(2)在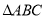 中,
中,  所对的边分别是
所对的边分别是 ,
,
 ,
,
求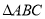 周长
周长 的最大值.
的最大值.
(1)最小正周期为 ,最大值是0;(2)6.
,最大值是0;(2)6.
【解析】
试题分析:(1)首先根据三角函数的恒等变换,变换成正弦型函数,然后求出函数的最小正周期和最值.(2)先根据上面的结论,求出A的值,再利用正弦定理求出三角形的周长,最后根据取值范围利用基本不等式或用三角函数可确定最值.
试题解析:(1)
 , 2分
, 2分
 最小正周期为
最小正周期为 4分
4分


所以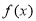 在区间
在区间 的最大值是0. 6分
的最大值是0. 6分
(2)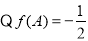 ,
, 8分
8分
由余弦定理得,

即 ,当且仅当
,当且仅当 时取等号.
时取等号.
 的周长的最大值是6. 12分
的周长的最大值是6. 12分
法二:由 ,得
,得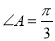 ,由正弦定理可得,
,由正弦定理可得,
 8分
8分
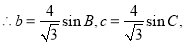

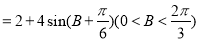
所以,当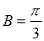 时,L取最大值,且最大值为6 . 12分
时,L取最大值,且最大值为6 . 12分
考点:1. 三角函数中的恒等变换应用;2. 三角函数的周期性及其求法.3.三角函数的最值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是 的重心,内角
的重心,内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,则角
,则角 的大小是 .
的大小是 .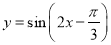 的图象向右平移
的图象向右平移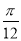 个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为
个单位,然后纵坐标不变横坐标伸长为原来的2倍,得到函数解析式为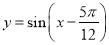
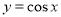
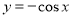
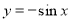
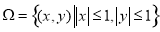 ,A是由直线
,A是由直线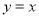 与曲线
与曲线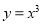 围成的封闭区域,用随机模拟的方法求A的面积时,先产生
围成的封闭区域,用随机模拟的方法求A的面积时,先产生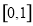 上的两组均匀随机数,
上的两组均匀随机数, 和
和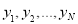 ,由此得N个点
,由此得N个点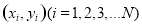 ,据统计满足
,据统计满足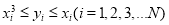 的点数是
的点数是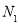 ,由此可得区域A的面积的近似值是( )
,由此可得区域A的面积的近似值是( )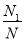 B.
B. 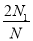 C.
C. 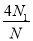 D.
D. 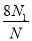
 则( )
则( ) B.
B. C.
C. D.
D.
 的边长为
的边长为 ,则
,则 ______;
______;
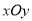 上的区域
上的区域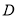 由不等式组
由不等式组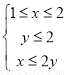 给定.若
给定.若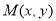 为
为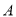 的坐标为
的坐标为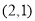 ,则
,则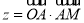 的最大值为( )
的最大值为( ) 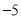 B.
B.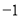 C.
C.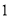 D.
D.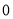
 ,若
,若 ,则
,则 .
. ,
, ,则
,则 的值为
的值为 (B)
(B) (C)
(C) (D)
(D)