题目内容
8.已知点M在不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y≥0}\\{x≤0}\end{array}\right.$所表示的平面区域内,点N在圆x2+y2+6x-4y+12=0上,则MN的最小值是$\frac{\sqrt{34}}{2}$-1.分析 化简可得(x+3)2+(y-2)2=1,从而作平面区域,结合图象可得MN的最小值是|MA|-1,从而解得.
解答 解:∵x2+y2+6x-4y+12=0,∴(x+3)2+(y-2)2=1,
作平面区域如下, ,
,
圆心A(-3,2),M(-$\frac{1}{2}$,$\frac{1}{2}$),
结合图象可知,
MN的最小值是|MA|-1
=$\sqrt{(-3+\frac{1}{2})^{2}+(2-\frac{1}{2})^{2}}$-1
=$\frac{\sqrt{34}}{2}$-1.
故答案为:$\frac{\sqrt{34}}{2}$-1.
点评 本题考查了数形结合的思想应用及学生的作图能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知集合A={x||x-1|≤1,x∈R},${B}=\left\{{x\left|{\sqrt{x}≤2,x∈{Z}}\right.}\right\}$,则A∩B=( )
| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
16.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | 若a,b∈R,则“ab≠0”是“a≠0”的充分不必要条件 | |
| C. | 命题“?x0∈R,x02+x0+1<0”的否定是“?x∈R,x2+x+1>0” | |
| D. | 若“p且q”为假,则p,q全是假命题 |
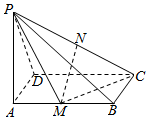 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.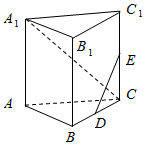 已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.
已知三棱柱ABC-A1B1C1,侧棱AA1垂直于底面ABC,∠$ABC=\frac{π}{2}$,AB=BC=AA1=4,D为BC的中点.