题目内容
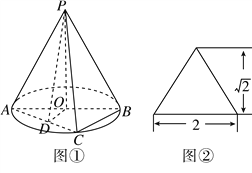
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)参考解析;(3)
;(2)参考解析;(3)![]()
【解析】试题分析:由圆锥的正视图可知,圆锥的底面直径为2,高为2,(1)所以圆锥的母线长![]() ,由圆锥的侧面积公式
,由圆锥的侧面积公式![]() .本小题的关键是应用根据三视图得到圆锥的半径以及圆锥的高,从而运用圆锥的侧面积公式.
.本小题的关键是应用根据三视图得到圆锥的半径以及圆锥的高,从而运用圆锥的侧面积公式.
(2)欲证平面PAC![]() 平面POD.由判定定理可知,转化为线面垂直.通过观察确定直线AC垂直平面PDO.由已知即可得到结论.
平面POD.由判定定理可知,转化为线面垂直.通过观察确定直线AC垂直平面PDO.由已知即可得到结论.
(3)点A到平面PCB的距离,,利用![]() ,分别计算出
,分别计算出![]() .即可得到点A到平面PCB的距离.
.即可得到点A到平面PCB的距离.
试题解析:(1)由正(主)视图可知圆锥的高![]() ,圆
,圆![]() 的直径为
的直径为![]() ,故半径
,故半径![]() .∴圆锥的母线长
.∴圆锥的母线长![]() ,
,
∴圆锥的侧面积![]() .
.
(2)证明:连接![]() ,∵
,∵![]() ,
, ![]() 为
为![]() 的中点,
的中点,
∴![]() .∵
.∵![]() ,
, ![]() ,∴
,∴![]() .又
.又![]() ,
,
∴![]() .又
.又![]() ,
,![]() 平面
平面![]() 平面
平面![]()
(3)![]() ,又
,又![]() ,
,![]() 利用等体积法可求出距离,
利用等体积法可求出距离, ![]()

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目