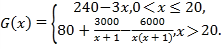题目内容
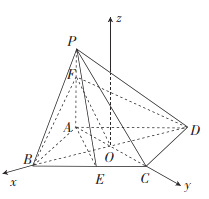
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上的一点.
上的一点.

(1)证明:平面![]() 平面
平面![]() .
.
(2)若![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由![]() 得
得![]() 平面PAE,进而可得证;
平面PAE,进而可得证;
(2)先证得![]() 平面
平面![]() ,设
,设![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() ,分别计算平面
,分别计算平面![]() 的法向量为
的法向量为![]() 和
和![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则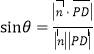 ,代入计算即可得解.
,代入计算即可得解.
(1)证明:连接![]() ,因为
,因为![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 为等边三角形,
为等边三角形,![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:设![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
同理可证![]() ,所以
,所以![]() 平面
平面![]() .
.
如图,设![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .
.
易知![]() 为二面角
为二面角![]() 的平面角,所以
的平面角,所以![]() ,从而
,从而![]() .
.
由![]() ,得
,得![]() .
.
又由![]() ,
,![]() ,知
,知![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得 ,不妨设
,不妨设![]() ,得
,得![]() .
.
又![]() ,
,![]() ,所以
,所以![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则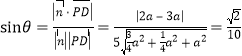 .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某电子科技公司由于产品采用最新技术,销售额不断增长,最近![]() 个季度的销售额数据统计如下表(其中
个季度的销售额数据统计如下表(其中![]() 表示
表示![]() 年第一季度,以此类推):
年第一季度,以此类推):
季度 |
|
|
|
|
|
季度编号x |
|
|
|
|
|
销售额y(百万元) |
|
|
|
|
|
(1)公司市场部从中任选![]() 个季度的数据进行对比分析,求这
个季度的数据进行对比分析,求这![]() 个季度的销售额都超过
个季度的销售额都超过![]() 千万元的概率;
千万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程,并预测该公司
的线性回归方程,并预测该公司![]() 的销售额.
的销售额.
附:线性回归方程:![]() 其中
其中 ,
,![]()
参考数据:![]() .
.
【题目】某专卖店为了对新产品进行合理定价,将该产品按不同的单价试销,调查统计如下表:
售价 | 4 | 5 | 6 | 7 | 8 |
周销量 | 90 | 85 | 83 | 79 | 73 |
(1)求周销量y(件)关于售价x(元)的线性回归方程![]() ;
;
(2)按(1)中的线性关系,已知该产品的成本为2元/件,为了确保周利润大于598元,则该店应该将产品的售价![]() 定为多少?
定为多少?
参考公式: ,
,![]() .
.
参考数据:![]() ,
,![]()