题目内容
8.已知△ABC和点M满足$\overrightarrow{MB}$+$\overrightarrow{MC}$=-$\overrightarrow{MA}$,若存在实数m使得m$\overrightarrow{AB}$+m$\overrightarrow{AC}$=$\overrightarrow{AM}$成立,则m等于( )| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
分析 作出图象,由向量加法的平行四边形法则可知M是△ABC的重心,故$\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AM}$,代入m$\overrightarrow{AB}$+m$\overrightarrow{AC}$=$\overrightarrow{AM}$可解出m.
解答 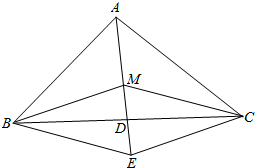 解:以MB,MC为邻边作平行四边形MBEC,连结ME交BC于D,如图.
解:以MB,MC为邻边作平行四边形MBEC,连结ME交BC于D,如图.
则$\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{ME}=2\overrightarrow{MD}$,∵$\overrightarrow{MB}$+$\overrightarrow{MC}$=-$\overrightarrow{MA}$,
∴M在线段AD上,且|MA|=2|MD|,∵D是BC中点,
∴$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AD}$=3$\overrightarrow{AM}$,
∵m$\overrightarrow{AB}$+m$\overrightarrow{AC}$=$\overrightarrow{AM}$,
∴3m$\overrightarrow{AM}$=$\overrightarrow{AM}$,
∴m=$\frac{1}{3}$.
故选C.
点评 本题考查了平面向量加法的平行四边形法则,确定M的位置是关键.

练习册系列答案
相关题目
19.已知三点A(2,2),B(3,1),C(-1,-1),则过点A的直线l与线段BC有公共点时(公共点包含公共点),直线l的斜率kl的取值范围是( )
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
20.函数f(x)=$\sqrt{2-x}$+$\sqrt{x}$的定义域为( )
| A. | (2,+∞) | B. | (-∞,0) | C. | (0,2) | D. | [0,2] |
 如图,在△ABC和△DBE中,$\frac{AB}{DB}=\frac{BC}{BE}=\frac{AC}{DE}=\frac{5}{3}$,若△ABC与△DBE的周长之差为10cm,则△ABC的周长为25cm.
如图,在△ABC和△DBE中,$\frac{AB}{DB}=\frac{BC}{BE}=\frac{AC}{DE}=\frac{5}{3}$,若△ABC与△DBE的周长之差为10cm,则△ABC的周长为25cm.