题目内容
已知a为实数, 。
。
⑴求导数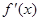 ;
;
⑵若 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
⑶若 在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
在(-∞,-2)和(2,+∞)上都是递增的,求a的取值范围。
⑴
⑵f(x)在[-2,2]上的最大值为 最小值为
最小值为
⑶a的取值范围是[-2,2].
解析试题分析:⑴由原式得 ∴
∴
⑵由 得
得 ,此时有
,此时有 .
.
由 得
得 或x="-1" , 又
或x="-1" , 又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为
⑶解法一: 的图象为开口向上且过点(0,-4)的抛物线,由条件得
的图象为开口向上且过点(0,-4)的抛物线,由条件得
即 ∴-2≤a≤2.
∴-2≤a≤2.
所以a的取值范围为[-2,2].
解法二:令 即
即 由求根公式得:
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时, 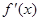 ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得-2≤a≤2.
解不等式组得-2≤a≤2.
∴a的取值范围是[-2,2].
考点:导数计算,利用导数研究函数的单调性、极值、最值。
点评:中档题,此类问题较为典型,是导数应用的基本问题。在某区间,导函数值非负,函数为增函数,导函数值非正,函数为减函数。求最值应遵循“求导数,求驻点,计算极值及端点函数值,比较确定最值”。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 时,求
时,求 在
在 上的最小值;
上的最小值; 上为增函数,求正实数
上为增函数,求正实数 的取值范围;
的取值范围; 的方程
的方程 在区间
在区间 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数 的取值范围.
的取值范围. ,
, .
. ,求
,求 的取值范围;
的取值范围; 的解集为R,求
的解集为R,求 的取值范围.
的取值范围. 在
在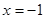 处取得极值
处取得极值 .
. .
. 的单调性;
的单调性; ,求
,求 为
为 内的任意两个值,试比较
内的任意两个值,试比较  与
与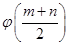 的大小.
的大小. .
. 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数 都有
都有 成立,试求
成立,试求 的取值范围;
的取值范围; .当
.当 时,函数
时,函数 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
 分钟应付话费y元,写出函数解析式并画出函数图象.
分钟应付话费y元,写出函数解析式并画出函数图象.
 有两个不同的交点,求实数m的取值范围.
有两个不同的交点,求实数m的取值范围. 
 时, 求函数
时, 求函数 的单调增区间;
的单调增区间; 时,求函数
时,求函数 上的最小值;
上的最小值;