题目内容
已知：P为椭圆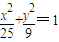
上的任意一点，过椭圆的右顶点A和上顶点B分别作与x轴和y 轴的平行线交于C，过P引BC、AC的平行线交AC于N，交BC于M，交AB于D、E，矩形PMCN是S1，三角形PDE的面积是S2，则S1：S2=（ ）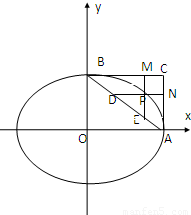
A．1
B．2
C．
D．与点P的坐标有关
【答案】分析：确定AB的方程，求出S△ADN、SACME．利用P（x，y）在椭圆上可知面积相等，从而可得结论．
解答：解：设P（x，y）在第一象限，则AB的方程为
，∴D（
，y），
∴S△ADN=
=
∵E（x，
），
∴SACME=
=
∵P（x，y）在椭圆上，∴
，
∴
，
∴
=
∴S△ADN=SACME
∵矩形PMCN是S1，三角形PDE的面积是S2，
∴S1：S2=1：1
故选A．
点评：本题考查椭圆的标准方程，考查面积的计算，考查学生的计算能力，属于中档题．
解答：解：设P（x，y）在第一象限，则AB的方程为
，∴D（，y），∴S△ADN=
=∵E（x，
），∴SACME=
=∵P（x，y）在椭圆上，∴
，∴
，∴
=∴S△ADN=SACME
∵矩形PMCN是S1，三角形PDE的面积是S2，
∴S1：S2=1：1
故选A．
点评：本题考查椭圆的标准方程，考查面积的计算，考查学生的计算能力，属于中档题．
练习册系列答案
互动英语系列答案
相关题目
均在椭圆
上，直线
、
分别过椭圆的左右焦点
、
，当
时，有
.
的方程;
是椭圆
为圆
的任一条直径，求
的最大值.
均在椭圆
上，直线
、
分别过椭圆的左右焦点
、
，当
时，有
.
的方程;
为圆
的任一条直径，求
的最大值.
，P为椭圆上除长轴端点外的任一点，F1，F2为椭圆的两个焦点．
；