题目内容
若实数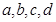 满足
满足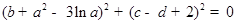 ,则
,则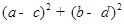 的最小值为( )
的最小值为( )
A.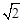 | B.2 | C.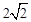 | D.8 |
D
解析试题分析: ,
,
设 为两动点,则点
为两动点,则点 是函数
是函数 的图象上一点,点
的图象上一点,点 是函数
是函数 的图象上一点;而
的图象上一点;而 ,
,
则问题转化为求曲线 上的点
上的点 到直线
到直线 的距离的最小值,如下图所示,
的距离的最小值,如下图所示,
直线 的斜率为1;
的斜率为1;
由 ,得
,得 ,令
,令 ,所以,
,所以, ,解之得:
,解之得: (舍去),
(舍去),
由 ,得
,得 ;所以
;所以 到直线
到直线 的距离最小
的距离最小
从而有 ,故选D.
,故选D.
考点:1.导数的应用;2、数形结合.

练习册系列答案
相关题目
定义在R上的函数 满足:
满足: 恒成立,若
恒成立,若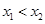 ,则
,则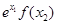 与
与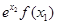 的大小关系为 ( )
的大小关系为 ( )
A. 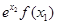 | B.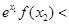 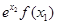 |
C.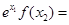 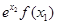 | D.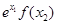 与 与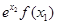 的大小关系不确定 的大小关系不确定 |
曲线y=cosx(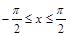 )与两坐标轴所围成的图形的面积为( )
)与两坐标轴所围成的图形的面积为( )
| A.4 | B.2 | C.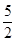 | D.3 |
设函数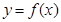 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数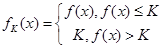 ,取函数
,取函数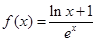 ,恒有
,恒有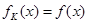 ,则( )
,则( )
A.K的最大值为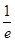 | B.K的最小值为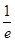 |
| C.K的最大值为2 | D.K的最小值为2 |
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
定义域为R的连续函数 ,对任意x都有
,对任意x都有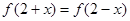 ,且其导函数
,且其导函数 满足
满足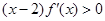 ,则当
,则当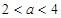 时,有( )
时,有( )
A. | B.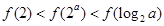 |
C.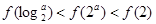 | D.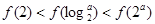 |
 的图象上的点
的图象上的点 处的切线的斜率为k,若
处的切线的斜率为k,若 ,则函数
,则函数
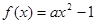 的图像在点A(1,f(1))处的切线l与直线
的图像在点A(1,f(1))处的切线l与直线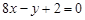 平行,若数列
平行,若数列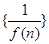 的前
的前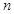 项和为
项和为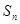 ,则
,则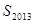 的值为( )
的值为( )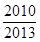


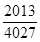
 的图象上;②点A、B关于原点对称,则点(A,B)是函数
的图象上;②点A、B关于原点对称,则点(A,B)是函数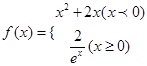 ,则
,则