题目内容
在正方体ABCD-A1B1C1D1中，M和N分别为BC、C1C的中点，那么异面直线MN与AC所成的角等于（ ）
| A、30° | B、45° |
| C、60° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：如图所示，连接BC1．则MN∥BC1．连接A1C1，A1B．利用正方体的性质可得AC∥A1C1，故∠BC1A1或其补角是异面直线MN与AC所成的角．再利用正方体的性质、等边三角形的性质即可得出．
解答：
解：如图所示，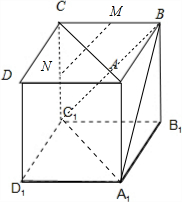
连接BC1．则MN∥BC1．
连接A1C1，A1B．
则AC∥A1C1，
∴∠BC1A1或其补角是异面直线MN与AC所成的角．
∵△A1BC1是等边三角形．
∴∠A1C1B=60°．
∴异面直线MN与AC所成的角是60°．
故选：C．
连接BC1．则MN∥BC1．连接A1C1，A1B．
则AC∥A1C1，
∴∠BC1A1或其补角是异面直线MN与AC所成的角．
∵△A1BC1是等边三角形．
∴∠A1C1B=60°．
∴异面直线MN与AC所成的角是60°．
故选：C．
点评：本题考查了正方体的性质、等边三角形的性质、三角形的中位线定理、异面直线所成的角，考查了推理能力，属于基础题．
练习册系列答案
相关题目
已知集合M={y|y=-2x+1，x∈R}，N={y|y=x-2，x∈R}，那么M∩N=（ ）
| A、（-1，1） |
| B、{（-1，1）} |
| C、{y|y=-1} |
| D、R |
函数f（x）=x2-2ax+2在（-∞，3）上递减，则a的取值范围是（ ）
| A、[-3，+∞） |
| B、（-∞，-3] |
| C、（-∞，3} |
| D、[3，+∞） |
复数z=
（i为虚数单位），则z的共轭复数z为（ ）
| 3+i |
| 1+i |
| A、2-i | B、2+i |
| C、4-2i | D、4+2i |