题目内容
如图所示，在四棱锥S-ABCD中，底面ABCD为平行四边形，E，F分别为AB，SC的中点，求证：EF∥平面SAD。
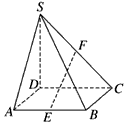
| 证明：取线段CD的中点M，连结ME，MF， ∵E，F分别为AB，SC的中点， ∴ME∥AD，MF∥SD， 又∵ME，MF  平面SAD，∴ME∥平面SAD，MF∥平面SAD， 又∵ME，MF相交， ∴平面MEF∥平面SAD， ∵EF  平面MEF，∴EF∥平面SAD。 |
 |
练习册系列答案
活力课时同步练习册系列答案
相关题目
活力课时同步练习册系列答案
如图所示，在四棱锥S-ABCD中，SD⊥底面ABCD，四边形ABCD为矩形，E，F分别为AB、SC的中点，且AD=SD=2，DC=3．
如图所示，在四棱锥S-ABCD中，BA⊥面SAD，CD⊥面SAD，SA⊥SD，且SA=SD=DC=2AB．O为AD中点．
（1）求证：AC⊥平面SBD；
如图所示，在四棱锥S-ABCD中，BA⊥面SAD，CD⊥面SAD，SA⊥SD，且SA=SD=DC=2AB．O为AD中点．
BC=1，E为SD中点．
BC，求证：EF//平面SAB；
，若存在，求出G点位置；若不存在，说明理由．