题目内容
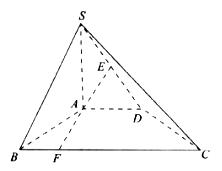
 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.(1)求证:SO⊥BC;
(2)求直线SO与面SBC所成的角.
分析:(1)由已知中BA⊥面SAD,由面面垂直的判断定理可得面ABCD⊥面SAD,由等腰三角形三线合一,可得SO⊥AD,结合面面垂直的性质定理可得SO⊥面ABCD,最后由线面垂直的性质定理得到SO⊥BC;
(2)过O作OE⊥BC于E,连SE,由三垂线定理,及线面夹角的定义,我们可得直角△SOE中,∠OSE为所求SO与面SBC所成的角,解直角△SOE,即可得到答案.
(2)过O作OE⊥BC于E,连SE,由三垂线定理,及线面夹角的定义,我们可得直角△SOE中,∠OSE为所求SO与面SBC所成的角,解直角△SOE,即可得到答案.
解答: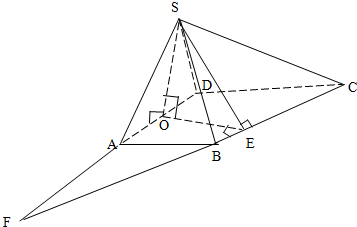 证明:(1)∵BA⊥面SAD,CD⊥面SAD
证明:(1)∵BA⊥面SAD,CD⊥面SAD
∴BA∥CD
∴面ABCD⊥面SAD(3分)
又SA=SD,O为AD中点,
∴SO⊥AD
∴SO⊥面ABCD
故SO⊥BC(5分)
解:(2)过O作OE⊥BC于E,连SE,则由三垂线定理,BC⊥SE.∴BC⊥面SOE
∴面SBC⊥面SOE,从而SE就是SO在面SBC上的射影
在直角△SOE中,∠OSE为所求SO与面SBC所成的角. (8分)
设AB=a,延长CB交DA延长线于F,则DA=2SO=2
a,DF=4
a,从而FC=6a.
∴由
=
得:OE=
•3
a=
a(10分)
∴tan∠OSE=
=1.即∠OSE=45°(12分)
 证明:(1)∵BA⊥面SAD,CD⊥面SAD
证明:(1)∵BA⊥面SAD,CD⊥面SAD∴BA∥CD
∴面ABCD⊥面SAD(3分)
又SA=SD,O为AD中点,
∴SO⊥AD
∴SO⊥面ABCD
故SO⊥BC(5分)
解:(2)过O作OE⊥BC于E,连SE,则由三垂线定理,BC⊥SE.∴BC⊥面SOE
∴面SBC⊥面SOE,从而SE就是SO在面SBC上的射影
在直角△SOE中,∠OSE为所求SO与面SBC所成的角. (8分)
设AB=a,延长CB交DA延长线于F,则DA=2SO=2
| 2 |
| 2 |
∴由
| OE |
| OF |
| DC |
| FC |
| 2a |
| 6a |
| 2 |
| 2 |
∴tan∠OSE=
| OE |
| SO |
点评:本题考查的知识点是平面与平面垂直的判定,平面与平面垂直的性质,直线与平面所成的角,其中(1)的关键是熟练掌握空间中线线垂直,线面垂直及面面垂直之间的相互转化,(2)的关键是构造出∠OSE为所求SO与面SBC所成的角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
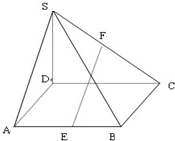 如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3.
如图所示,在四棱锥S-ABCD中,SD⊥底面ABCD,四边形ABCD为矩形,E,F分别为AB、SC的中点,且AD=SD=2,DC=3.
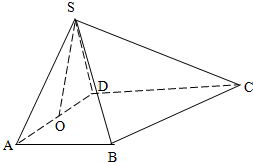 如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.
如图所示,在四棱锥S-ABCD中,BA⊥面SAD,CD⊥面SAD,SA⊥SD,且SA=SD=DC=2AB.O为AD中点.