题目内容
已知锐角△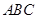 三个内角分别为
三个内角分别为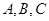 向量
向量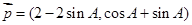 与向量
与向量 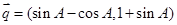 是共线向量.
是共线向量.
(1)求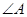 的值;
的值;
(2)求函数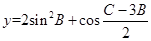 的值域.
的值域.
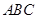 三个内角分别为
三个内角分别为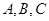 向量
向量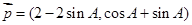 与向量
与向量 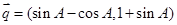 是共线向量.
是共线向量.(1)求
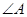 的值;
的值;(2)求函数
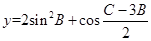 的值域.
的值域.(1)A=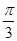 . (2)y∈
. (2)y∈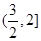
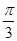 . (2)y∈
. (2)y∈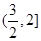
考查向量共线的坐标表示,∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A),求函数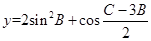 的值域需将函数化为一角一名称的形式,y=sin(2B-
的值域需将函数化为一角一名称的形式,y=sin(2B- )+1.再用整体法,得出整体角的范围∴2B-
)+1.再用整体法,得出整体角的范围∴2B- ∈(
∈( ,
,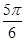 ).
).
解:(1)∵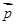 ,
,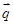 共线,
共线,
∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A), ……1分
∴sin2A=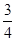 . ………3分
. ………3分
又△ABC为锐角三角形∴sin A=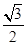 ,∴A=
,∴A=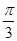 . …………5分
. …………5分
(2)y=2sin2B+cos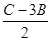 =2sin2B+cos
=2sin2B+cos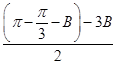 …………………6分
…………………6分
=2sin2B+cos(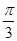 -2B)=1-cos 2B+
-2B)=1-cos 2B+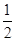 cos 2B+
cos 2B+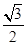 sin 2B …………8分
sin 2B …………8分
=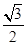 sin 2B-
sin 2B-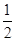 cos 2B+1=sin(2B-
cos 2B+1=sin(2B- )+1. …………10分
)+1. …………10分
∵B∈(0,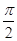 ),又因为B+A>
),又因为B+A>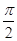 ∴
∴ <B<
<B<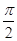 ∴2B-
∴2B- ∈(
∈( ,
,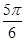 ). ……11分
). ……11分
∴y∈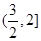
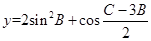 的值域需将函数化为一角一名称的形式,y=sin(2B-
的值域需将函数化为一角一名称的形式,y=sin(2B- )+1.再用整体法,得出整体角的范围∴2B-
)+1.再用整体法,得出整体角的范围∴2B- ∈(
∈( ,
,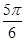 ).
).解:(1)∵
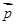 ,
,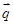 共线,
共线,∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A), ……1分
∴sin2A=
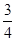 . ………3分
. ………3分又△ABC为锐角三角形∴sin A=
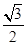 ,∴A=
,∴A=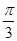 . …………5分
. …………5分(2)y=2sin2B+cos
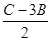 =2sin2B+cos
=2sin2B+cos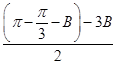 …………………6分
…………………6分=2sin2B+cos(
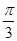 -2B)=1-cos 2B+
-2B)=1-cos 2B+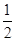 cos 2B+
cos 2B+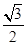 sin 2B …………8分
sin 2B …………8分=
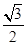 sin 2B-
sin 2B-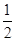 cos 2B+1=sin(2B-
cos 2B+1=sin(2B- )+1. …………10分
)+1. …………10分∵B∈(0,
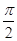 ),又因为B+A>
),又因为B+A>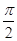 ∴
∴ <B<
<B<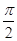 ∴2B-
∴2B- ∈(
∈( ,
,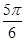 ). ……11分
). ……11分∴y∈

练习册系列答案
相关题目
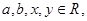 且
且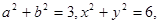 求
求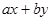 的最大值.
的最大值.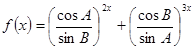 ,
,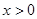 时,
时,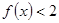 .
.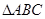 中,角
中,角 ,
,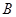 ,
,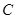 所对的边长分别是
所对的边长分别是 ,
,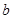 ,
,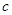 . 满足
. 满足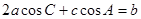 .
.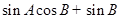 的最大值.
的最大值.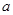 ,
,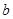 ,
,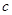 ,
,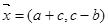 ,
,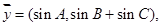
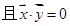 ,
,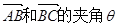 ;
; ,求
,求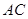 边上的高
边上的高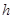 .
.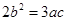 ,求A。
,求A。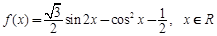 .]
.]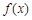 的最小值和最小正周期;
的最小值和最小正周期;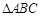 的内角
的内角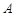 、
、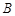 、
、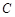 的对边分别为
的对边分别为 ,
,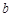 ,
,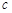 ,且
,且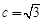 ,
,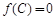 ,
,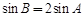 ,求
,求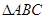 的内角
的内角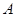 、
、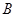 、
、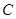 的对边分别为
的对边分别为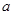 、
、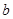 、
、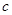 ,
,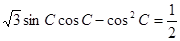 ,且
,且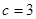
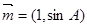 与
与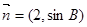 共线,求
共线,求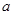 ,
,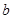 ,
,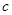 分别为
分别为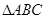 三个内角
三个内角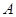 ,
,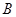 ,
,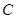 的对边,
的对边,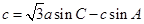 .
.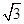 ,求
,求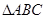 中,
中, 分别是角
分别是角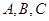 的对边,若
的对边,若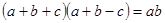 ,则
,则 = .
= .