题目内容
(1)设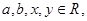 且
且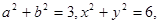 求
求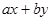 的最大值.
的最大值.
(2) △ABC是锐角三角形,函数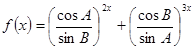 ,
,
证明: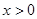 时,
时,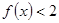 .
.
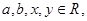 且
且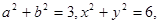 求
求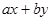 的最大值.
的最大值.(2) △ABC是锐角三角形,函数
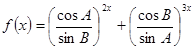 ,
,证明:
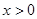 时,
时,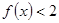 .
.(1) .
.
或三角换元. .
.
(2)见解析。
 .
.或三角换元.
 .
.(2)见解析。
(1) .然后问题基本得以解决.
.然后问题基本得以解决.
(2)解本小题的关键是由△ABC是锐角三角形,得 ,
, ,
,
同理 ,从而可得
,从而可得 ,后面问题易证.
,后面问题易证.
(1)解法1:
当且仅当 时取等号,所以
时取等号,所以 .
.
如取 .
.
解法2:三角换元. .
.
(2)△ABC是锐角三角形,故 ,
, ,
,
同理 ,
, .
.
又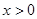 ,
, ,所以
,所以 .
.
 .然后问题基本得以解决.
.然后问题基本得以解决.(2)解本小题的关键是由△ABC是锐角三角形,得
 ,
, ,
,同理
 ,从而可得
,从而可得 ,后面问题易证.
,后面问题易证.(1)解法1:

当且仅当
 时取等号,所以
时取等号,所以 .
.如取
 .
.解法2:三角换元.
 .
.(2)△ABC是锐角三角形,故
 ,
, ,
,同理
 ,
, .
.又
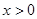 ,
, ,所以
,所以 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的大小;
的大小; 的取值范围.
的取值范围.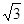 ,
,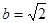 ,B=450求A、C及c.
,B=450求A、C及c.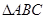 中,
中,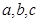 分别为内角
分别为内角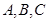 所对的边,且满足
所对的边,且满足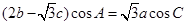 .
.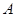 ;
;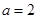 ②
②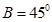 ③
③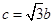 .从中选出两个可以确定
.从中选出两个可以确定
 的观礼台上,某一列座位所在直线
的观礼台上,某一列座位所在直线 与旗杆所在直线
与旗杆所在直线 共面,在该列的第一个座位
共面,在该列的第一个座位 和最后一个座位
和最后一个座位 测得旗杆顶端
测得旗杆顶端 的仰角分别为
的仰角分别为 和
和 ,且座位
,且座位 米,则旗杆的高度为_______________ 米
米,则旗杆的高度为_______________ 米 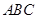 三个内角分别为
三个内角分别为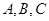 向量
向量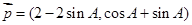 与向量
与向量 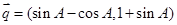 是共线向量.
是共线向量.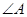 的值;
的值;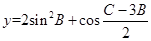 的值域.
的值域.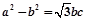 ,
,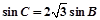 ,则角A= .
,则角A= .  ,
, ,S△ABC=4
,S△ABC=4 ,那么
,那么 =( )
=( )



 中,
中, ,那么角A等于( )
,那么角A等于( )