题目内容
若直线 始终平分圆
始终平分圆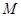 :
: 的周长,则
的周长,则 的最小值为 ( )
的最小值为 ( )
| A.8 | B.12 | C.16 | D.20 |
C
解析试题分析:因为,直线 始终平分圆
始终平分圆 的周长,所以圆心(-4,-1)在直线
的周长,所以圆心(-4,-1)在直线 上,从而,4a+b=1,
上,从而,4a+b=1,
所以,
 ,故选C。
,故选C。
考点:本题主要考查直线与圆的位置关系,均值定理的应用。
点评:小综合题,本解法通过“1”的代换,创造了应用均值定理的条件。应用均值定理,“一正,二定,三相等”缺一不可。

练习册系列答案
相关题目
当x>1时,不等式x-2+ ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围是 ( )
的取值范围是 ( )
| A.(-∞,0] | B.[0,+∞) | C.[1,+∞) | D.(-∞,1] |
设 、
、 为正数,则
为正数,则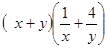 的最小值为( )
的最小值为( )
A. | B.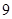 | C.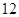 | D. |
已知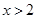 ,则函数
,则函数 的最小值是( )
的最小值是( )
| A.5 | B.4 | C.8 | D.6 |
已知正实数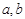 ,且
,且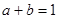 ,则
,则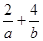 的最小值为 ( )
的最小值为 ( )
A.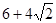 | B.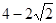 | C.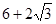 | D.5 |
函数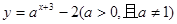 的图像恒过定点A,且点A在直线
的图像恒过定点A,且点A在直线 上
上 ,则
,则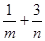 的最小值为( )
的最小值为( )
| A.12 | B.10 | C.8 | D.14 |
若函数f(x)=x+ (x>2)在
(x>2)在 处取最小值,则
处取最小值,则
A. | B. | C.3 | D.4 |
若正数 满足
满足 ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
已知 为正实数,且
为正实数,且 ,若
,若 对于满足条件的
对于满足条件的 恒成立,则
恒成立,则 的取值范围为
的取值范围为
A. | B. | C. | D. |