题目内容
已知椭圆E：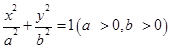
的离心率
，并且经过定点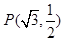
（1）求椭圆E 的方程；
（2）问是否存在直线y=-x+m，使直线与椭圆交于A, B 两点，满足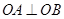
,若存在求m 值，若不存在说明理由．
（1）
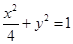;（2）
．
解析试题分析：（1）利用椭圆E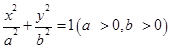：的离心率，并且经过定点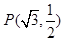，建立方程，求出a，b，即可求椭圆E的方程；（2）直线y=-x+m代入椭圆方程，利用韦达定理，结合OA⊥OB⇒
，即可求m值．
试题解析：解（1）由题意：
且
，又
解得：
，即：椭圆E的方程为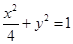
（2）设
（*）
所以
由
得
又方程（*）要有两个不等实根，
m的值符合上面条件，所以
考点：直线与圆锥曲线的综合问题．
练习册系列答案
相关题目
已知点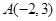
在抛物线
的准线上，过点
的直线与
在第一象限相切于点
，记的焦点为
，则
的值为
| A．3 | B．4 | C．5 | D．6 |
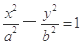
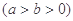的左焦点为F，过F作圆
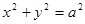的切线，切点为E，延长FE交双曲线右支于点P，若E为PF的中点，则双曲线的离心率为 （ ）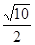
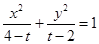所表示的曲线为C，有下列命题：
；
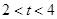或
；
上的双曲线，则
，离心率为
的椭圆的标准方程为________．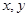
的取值如下表所示，若
与
线性相关，且
，则
（ ）
C．
D．
某市对上下班交通情况作抽样调查，作出上下班时间各抽取 的12辆机动车行驶时速（单位：km/h）的茎叶图如图.则上、下班行驶时速的中位数分别为（）
| A．28与28.5 | B．29与28.5 | C．28与27.5 | D．29与27.5 |
的平均数是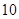
，标准差是
，则
