题目内容

函数y=
log
1
2
tanx
的定义域为（　　）
分析：依题意，解不等式0＜tanx≤1即可求得答案．
解答：解：依题意，得log
1
2
tanx≥0
∴0＜tanx≤1，
∴kπ＜x≤kπ+
π
4
，k∈Z
∴函数y=
log
1
2
tanx
的定义域为{x|kπ＜x≤kπ+
π
4
，k∈Z}．
故选C．
点评：本题考查正切函数的单调性，考查对数函数的性质与解不等式的能力，属于中档题．
练习册系列答案
相关题目
函数y=
1-2x
+x的值域是
 
．
函数y=
lgx+1
x-1
的定义域为
 
．
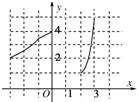13、函数y=f（x）的图象如图所示．那么，f（x）的定义域是
[-3，0]∪[2，3]
；值域是
[1，5]
；其中只与x的一个值对应的y值的范围是
[1，2）∪（4，5]
．
已知向量
an
=(cos
nπ
7
，sin
nπ
7
)，|
b
|=1．则函数y=|
a1
+
b
|2+|
a2
+
b
|2+|
a3
+
b
|2+…+|
a141
+
b
|2的最大值为
 
．
已知函数y=f（x）的图象如图，f（-
12
）=1，求函数y=f（x）的解析式．
精英家教网

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网