题目内容
下列函数中，既是奇函数又是减函数的是（ ）
A． | B． |
C． | D． |
D
解析试题分析：对与幂函数
，定义域为
，
，函数
为奇函数，但是函数在
上为增函数，A选项不对；对于函数
，定义域为
，它为奇函数，它在每个区间
上均为减函数，但是函数在定义域上不是减函数；对于C选项，函数
的定义域为
，关于原点对称，
，函数为奇函数，
但是
，
，故
，故函数在定义域上不是减函数，由排除法答案选D.
考点：函数单调性与奇偶性
练习册系列答案
相关题目
若函数
在区间
，0)内单调递增，则
取值范围是( )
A．[ ，1) | B．[ ，1) | C． ， | D．(1， ) |
若函数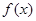
的零点与
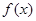的零点之差的绝对值不超过0.25，则可以是（ ）
A． | B． |
C． | D． |
的图象如右图所示，则函数
的可能图象是( )
已知
，则函数
的零点的个数为（ ）
| A．1 | B．2 | C．3 | D．4 |
已知直线
：
．若存在实数
使得一条曲线与直线有两个不同的交点，且以这两个交点为端点的线段长度恰好等于
，则称此曲线为直线的“绝对曲线”．下面给出四条曲线方程：①
；②
；③
；④
；则其中直线的“绝对曲线”有 （ ）
| A．①④ | B．②③ | C．②④ | D．②③④ |
的图象如图所示，则其导函数
的图象可能是（ ）
函数
,满足
,则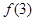
的值为（ ）
A． | B． 8 | C． 7 | D． 2 |