题目内容
若函数
 在区间
在区间 ,0)内单调递增,则
,0)内单调递增,则 取值范围是( )
取值范围是( )
A.[ ,1) ,1) | B.[ ,1) ,1) | C. , , | D.(1, ) ) |
B
解析试题分析:函数
 的定义域满足
的定义域满足 >0,∵x<0,∴
>0,∵x<0,∴ <0=>
<0=> ,
,
设y= ,y'=
,y'= -a=0,x=
-a=0,x= ,y'>0,x<
,y'>0,x< ,y'<0,x>
,y'<0,x> ,
,
∴ x∈( ,
, )时,y为增函数,x∈(
)时,y为增函数,x∈( ,
, )时,y为减函数,
)时,y为减函数,
∵x∈ ,0)时,
,0)时, 为增函数,∴0<
为增函数,∴0< <1且
<1且 <
< ,
, >0,
>0,
∴ <a<1.
<a<1.
考点:复合函数的单调性以及函数单调性与导数的关系.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知定义在 上的函数
上的函数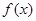 是偶函数,对
是偶函数,对 都有
都有 ,当
,当 时,
时, 的值为( )
的值为( )
| A.-2 | B.2 | C.4 | D.-4 |
若 在
在 上是减函数,则
上是减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( )
| A.1 | B. | C.3 | D. |
已知函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A. R, R, |
B.函数 的图像是中心对称图形 的图像是中心对称图形 |
C.若 是 是 的极小值点,则 的极小值点,则 在区间 在区间 上单调递减 上单调递减 |
D.若 是 是 的极值点,则 的极值点,则 |
下列函数中,既是奇函数又是减函数的是( )
A. | B. |
C. | D. |





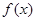 是定义在
是定义在 上的奇函数,若对于任意的实数
上的奇函数,若对于任意的实数 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 的值为 ( )
的值为 ( )



 在点
在点 处的切线的斜率为
处的切线的斜率为 ,则函数
,则函数 的部分图象可以为( )
的部分图象可以为( )