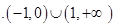题目内容
已知直线 :
:
 .若存在实数
.若存在实数 使得一条曲线与直线
使得一条曲线与直线 有两个不同的交点,且以这两个交点为端点的线段长度恰好等于
有两个不同的交点,且以这两个交点为端点的线段长度恰好等于 ,则称此曲线为直线
,则称此曲线为直线 的“绝对曲线”.下面给出四条曲线方程:①
的“绝对曲线”.下面给出四条曲线方程:① ;②
;② ;③
;③ ;④
;④ ;则其中直线
;则其中直线 的“绝对曲线”有 ( )
的“绝对曲线”有 ( )
| A.①④ | B.②③ | C.②④ | D.②③④ |
D
解析试题分析:由题意直线 表示斜率为
表示斜率为 且过定点(1,1)的直线.(1)曲线①是由左右两支射线构成:
且过定点(1,1)的直线.(1)曲线①是由左右两支射线构成: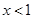 时,是斜率为2且过点(1,0)的射线;
时,是斜率为2且过点(1,0)的射线;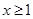 时,是斜率为-2且过点(1,0)的射线.作图可知:当
时,是斜率为-2且过点(1,0)的射线.作图可知:当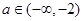 ,直线
,直线 仅与曲线①右支射线有一个交点;当
仅与曲线①右支射线有一个交点;当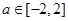 时,直线
时,直线 与曲线①无交点;当
与曲线①无交点;当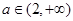 时,直线
时,直线 仅与曲线①左支射线有一个交点.所以直线
仅与曲线①左支射线有一个交点.所以直线 与曲线①最多只有一个交点,不符题意,故曲线①不是直线
与曲线①最多只有一个交点,不符题意,故曲线①不是直线 的“绝对曲线”.(2)因为定点(1,1)在曲线②上,所以直线
的“绝对曲线”.(2)因为定点(1,1)在曲线②上,所以直线 与曲线②恒有交点,设曲线②与直线
与曲线②恒有交点,设曲线②与直线 的两交点为
的两交点为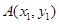 、
、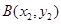 ,易知
,易知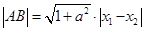
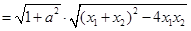 ,联立直线
,联立直线 与曲线②方程,化简得:
与曲线②方程,化简得: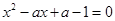 .
.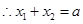
,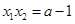 .
.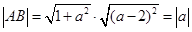 ,从而可知当且仅当
,从而可知当且仅当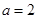 时直线
时直线 与曲线②仅一个交点.两边平方,化简得:
与曲线②仅一个交点.两边平方,化简得: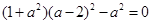 .设
.设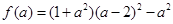 ,则
,则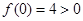 ,
,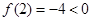 ,且
,且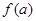 是连续函数,所以
是连续函数,所以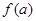 在(0,2)上有零点,即方程
在(0,2)上有零点,即方程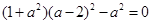 在(0,2)上有根,且在(0,2)上曲线②与直线
在(0,2)上有根,且在(0,2)上曲线②与直线 有两个不同的交点.故存在实数
有两个不同的交点.故存在实数 使得曲线②与直线
使得曲线②与直线 两个不同交点为端点的线段长度恰好等于
两个不同交点为端点的线段长度恰好等于 ,故曲线②是直线
,故曲线②是直线 的“绝对曲线”.(3)曲线③表示圆心在(1,1)且半径为1的圆,它与直线
的“绝对曲线”.(3)曲线③表示圆心在(1,1)且半径为1的圆,它与直线 两个交点为端点的线段长度恒为2,
两个交点为端点的线段长度恒为2, 为2或-2时满足题意,故曲线③是直线
为2或-2时满足题意,故曲线③是直线 的“绝对曲线”.(4)因为定点(1,1)在曲线④上,所以直线
的“绝对曲线”.(4)因为定点(1,1)在曲线④上,所以直线 与曲线④恒有交点,设曲线④与直线
与曲线④恒有交点,设曲线④与直线 的两交点为
的两交点为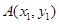 、
、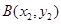 ,易知
,易知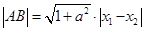
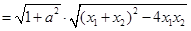 ,联立直线
,联立直线 与曲线④方程,化简得:
与曲线④方程,化简得: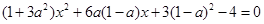
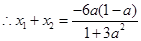 ,
, ,
,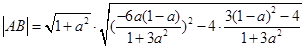
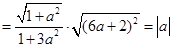 ,从而可知当且仅当
,从而可知当且仅当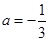 时直线
时直线 与曲线④仅一个交点.两边平方,化简得:
与曲线④仅一个交点.两边平方,化简得: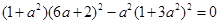 .
.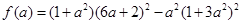 ,
,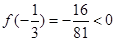 ,
,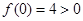 ,且
,且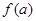 是连续函数,所以
是连续函数,所以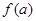 在
在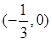 上有零点,即方程
上有零点,即方程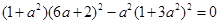 在
在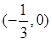 上有根,且在
上有根,且在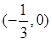 上曲线④与直线
上曲线④与直线 有两个不同的交点.故存在实数
有两个不同的交点.故存在实数 使得曲线④与直线
使得曲线④与直线 两个交点为端点的线段长度恰好等于
两个交点为端点的线段长度恰好等于 ,故曲线④是直线
,故曲线④是直线 的“绝对曲线”.
的“绝对曲线”.
考点:曲线与直线的方程、函数的零点

 名校课堂系列答案
名校课堂系列答案已知函数 (
( 为常数)是奇函数,则实数
为常数)是奇函数,则实数 为( )
为( )
| A.1 | B. | C.3 | D. |
若函数f(x) (x∈R)是奇函数,函数g(x) (x∈R)是偶函数,则 ( )
A.函数f(x) g(x)是偶函数 g(x)是偶函数 | B.函数f(x) g(x)是奇函数 g(x)是奇函数 |
| C.函数f(x)+g(x)是偶函数 | D.函数f(x)+g(x)是奇函数 |
若定义在R上的偶函数 满足
满足 且
且 时,
时, 则方程
则方程 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |
下列函数中,既是奇函数又是减函数的是( )
A. | B. |
C. | D. |
函数 零点的个数是 ( )
零点的个数是 ( )
A. | B.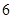 | C. | D.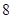 |
 中,
中, ,且
,且 ,设
,设 ,以
,以 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 为焦点且过点
为焦点且过点 的椭圆的离心率为
的椭圆的离心率为 ,设
,设 =
= 则
则 的大致图像是( )
的大致图像是( )

 在区间
在区间 上的简图是( )
上的简图是( )
 上为增函数,且
上为增函数,且 ,则不等式
,则不等式 的解集为( ).
的解集为( ).