题目内容
已知函数![]() ,设
,设![]() .
.
(Ⅰ)求![]() 的最小值;
的最小值;
(Ⅱ)若以![]() 图象上任意一点
图象上任意一点![]() 为切点的切线的斜率
为切点的切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
解.(Ⅰ) ![]()
![]()
![]()
![]()
由![]() .
.
所以当![]() 时,
时,![]() 的最小值为
的最小值为![]() ……4分
……4分
(Ⅱ)![]() ,
,![]() 恒成立。
恒成立。
所以![]() ,当
,当![]() 时
时![]() 有最大值
有最大值![]()
结合已知条件得![]() 。 …………8分
。 …………8分
(Ⅲ)若![]() 的图象与
的图象与
![]() 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即![]() 有四个不同的根,亦即
有四个不同的根,亦即
![]() 有四个不同的根. …………10分
有四个不同的根. …………10分
令![]() ,
,
则![]()
当![]() 变化时
变化时![]() 的变化情况如下表:
的变化情况如下表:
|
|
| (-1,0) | (0,1) | (1, |
|
| + | - | + | - |
|
| ↗ | ↘ | ↗ | ↘ |
由表格知:![]()
由上表可知,当![]() 时,
时,![]()
![]()
![]()
![]()

练习册系列答案
相关题目
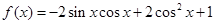
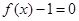 在(0,
在(0,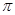 )内有两个零点
)内有两个零点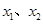 ,求
,求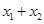 的值;
的值;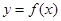 的图像向左移动
的图像向左移动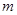
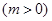 个单位,再向下平移2个单位,使所得函数的图象关于
个单位,再向下平移2个单位,使所得函数的图象关于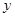 轴对称,求
轴对称,求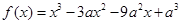 .
.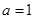 ,求函数
,求函数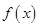 的极值;
的极值;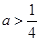 ,且当
,且当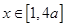 时,
时,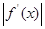
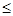 12a恒成立,试确定
12a恒成立,试确定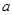 的取值范围.
的取值范围.