题目内容
若方程Ax2+By2=1表示焦点在x轴上的椭圆，则A、B满足的条件是
- A.B＞A
- B.A＞B＞0
- C.B＞A＞0
- D.A≠B，且A＞0，B＞0
C
分析：将椭圆化成焦点在x轴的标准方程的形式，可得x平方的分母大于y平方的分母，且两个分母均为正数，由此建立不等式关系，化简整理即得本题的答案．
解答：∵方程Ax2+By2=1表示焦点在x轴上的椭圆，
∴椭圆方程化为
，可得
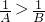，解之得B＞A＞0
故选：C
点评：本题给出曲线方程表示焦点在x轴的椭圆，求参数A、B的大小关系，着重考查了对椭圆的标准方程的认识，属于基础题．
分析：将椭圆化成焦点在x轴的标准方程的形式，可得x平方的分母大于y平方的分母，且两个分母均为正数，由此建立不等式关系，化简整理即得本题的答案．
解答：∵方程Ax2+By2=1表示焦点在x轴上的椭圆，
∴椭圆方程化为
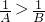，可得，解之得B＞A＞0故选：C
点评：本题给出曲线方程表示焦点在x轴的椭圆，求参数A、B的大小关系，着重考查了对椭圆的标准方程的认识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若方程Ax2+By2=1表示焦点在y轴上的双曲线，则A、B满足的条件是（ ）
| A、A＞0，且B＞0 | B、A＞0，且B＜0 | C、A＜0，且B＞0 | D、A＜0，且B＜0 |
＞