题目内容
7.在正四棱锥P-ABCD中,AB=6,二面角P-BC-A的大小为$\frac{π}{3}$,则异面直线PB与AD所成角的正弦值为( )| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 求出正四棱锥P-ABCD的高为3$\sqrt{3}$,P到BC的距离为6,PB=$\sqrt{9+36}$=3$\sqrt{5}$,利用AD∥BC,可得∠PBC是异面直线PB与AD所成角,即可得出结论.
解答 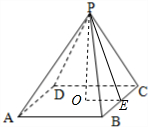 解:由题意,作出PO⊥平面ABCD,PE⊥BC,连接OE,
解:由题意,作出PO⊥平面ABCD,PE⊥BC,连接OE,
∵正四棱锥P-ABCD中,AB=6,二面角P-BC-A的大小为$\frac{π}{3}$,
∴正四棱锥P-ABCD的高为PO=3$\sqrt{3}$,P到BC的距离为PE=6,
∴PB=$\sqrt{9+36}$=3$\sqrt{5}$,
∵AD∥BC,
∴∠PBC是异面直线PB与AD所成角,
∴sin∠PBC=$\frac{6}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$,
故选B.
点评 本题考查面面角、线线角,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
17.若$tan({α+\frac{π}{4}})=2$,则$\frac{sinα-cosα}{sinα+cosα}$=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
18.阅读如图所示的程序框图,运行相应的程序,输出的S的值等于( )


| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
15.设函数f(x)=ax+bx+cx,其中c>a>0,c>b>0,若a,b,c是△ABC的三条边长,则下列结论正确的是( )
①对任意x∈(-∞,1),都有f(x)<0;
②存在x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,存在x∈(1,2),使f(x)=0.
①对任意x∈(-∞,1),都有f(x)<0;
②存在x∈R,使ax,bx,cx不能构成一个三角形的三条边长;
③若△ABC为钝角三角形,存在x∈(1,2),使f(x)=0.
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
2.在等差数列{an}中,已知a2=-8,公差d=2,则a12=( )
| A. | 10 | B. | 12 | C. | 14 | D. | 16 |
19.已知函数f(x)的导函数f'(x)的图象如图所示,则( )


| A. | x=-3为f(x)的极大值点 | B. | x=1为f(x)的极大值点 | ||
| C. | x=-1.5为f(x)的极大值点 | D. | x=2.5为f(x)的极小值点 |