题目内容

3．一个几何体的三视图如图所示（单位：m），则该几何体的体积为$4\sqrt{3}+1$m3．

分析 由题意，直观图是三棱柱与三棱锥的组合体，利用所给数据，求出体积．

解答 解：由题意，直观图是三棱柱与三棱锥的组合体，体积为$\frac{1}{2}×2×\sqrt{3}×4$+$\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}$=$4\sqrt{3}+1$．
故答案为：$4\sqrt{3}+1$．

点评 本题考查了棱锥的三视图和结构特征，属于基础题．

练习册系列答案
相关题目
13．已知点A在椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上，点P满足$\overrightarrow{AP}=（{λ-1}）\overrightarrow{OA}（{λ∈R}）$，且$\overrightarrow{OA}•\overrightarrow{OP}=72$，则线段OP在x轴上的投影长度的最大值为15．
14．已知函数f（x）=alnx+blog2x+1，f（2017）=3，则$f（\frac{1}{2017}）$等于（　　）
A．-1B．2C．-2D．$\frac{1}{4}$
11．三棱锥S-ABC中，AB=BC=AC=2，SC=4，SA=SB，SC与平面ABC所成角的余弦值是$\frac{{\sqrt{3}}}{3}$，若S，A，B，C都在同一球面上，则该球的表面积是（　　）
A．4πB．8πC．16πD．64π
18．已知函数$f（x）=alnx+\frac{x^2}{2}-（a-1）x，a∈R$．
（1）若函数f（x）在区间（1，3）上单调递减，求a的取值范围；
（2）当a=-1时，证明：$f（x）≥\frac{1}{2}$．
8．运行如图所示的程序框图，则输出的a、b、c满足（　　）
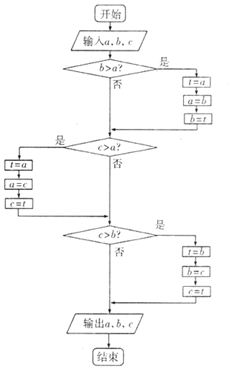
A．c≤b≤aB．a≤b≤cC．a≤c≤bD．b≤c≤a
15．执行如图所示的程序框图，则输出的i的值为（　　）
A．5B．6C．7D．8
12．若实数x，y满足约束条件$\left\{\begin{array}{l}2x-y-2≤0\\ 2x+y-4≥0\\ y≤2\end{array}\right.$则$\frac{y}{x}$的取值范围是  （　　）
A．$[{\frac{2}{3}，2}]$B．$[{\frac{1}{2}，\frac{3}{2}}]$C．$[{\frac{3}{2}，2}]$D．[1，2]
13．若不等式|x-t|＜1成立的必要条件是1＜x≤4，则实数t的取值范围是（　　）
A．[2，3]B．（2，3]C．[2，3）D．（2，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网