题目内容
(14分)已知函数
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
【答案】
(1)在区间(0,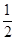 ),(1,+∞)上函数
),(1,+∞)上函数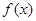 为减函数;在区间(
为减函数;在区间(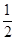 ,1)上函数
,1)上函数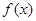 为增函数.(2)
为增函数.(2)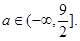
【解析】
试题分析:(1)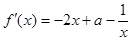 …………1分
…………1分
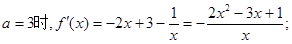
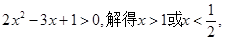 ……………………………4分
……………………………4分
函数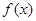 的定义域为(0,+∞),在区间(0,
的定义域为(0,+∞),在区间(0,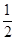 ),(1,+∞)上f ′(x)<0. 函数
),(1,+∞)上f ′(x)<0. 函数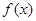 为减函数;在区间(
为减函数;在区间(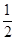 ,1)上f ′(x)>0. 函数
,1)上f ′(x)>0. 函数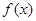 为增函数. ……………6分
为增函数. ……………6分
(2)函数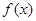 在(2,4)上是减函数,则
在(2,4)上是减函数,则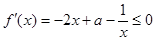 ,在x∈(2,4)上恒成立. …………7分
,在x∈(2,4)上恒成立. …………7分
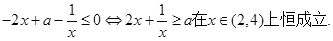 ………………10分
………………10分
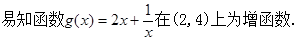
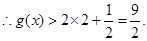 …………………12分
…………………12分
实数a的取值范围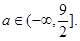 …………………………14分
…………………………14分
考点:利用导数研究函数的单调性。
点评:(1)在利用导数求函数的单调区间时,一定要先求函数的定义域。
(2)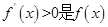 为单调递增函数的充分非必要条件。
为单调递增函数的充分非必要条件。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
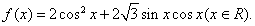
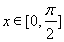
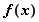

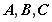
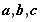
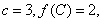
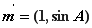
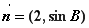
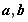

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
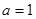 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.