题目内容
平面直角坐标系xOy中,过椭圆M: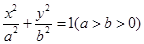 右焦点的直线
右焦点的直线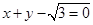 交
交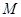 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为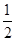 .
.
(Ι)求M的方程;
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形面积的最大值
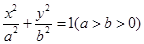 右焦点的直线
右焦点的直线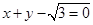 交
交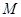 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为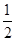 .
.(Ι)求M的方程;
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形面积的最大值
(Ι)  (Ⅱ)
(Ⅱ)

 (Ⅱ)
(Ⅱ)

(Ι)设
 则
则 ,
, ,(1)-(2)得:
,(1)-(2)得:
 ,因为
,因为 ,设
,设 ,因为P为AB的中点,且OP的斜率为
,因为P为AB的中点,且OP的斜率为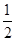 ,所以
,所以 ,即
,即 ,所以可以解得
,所以可以解得 ,即
,即 ,即
,即 ,又因为
,又因为 ,所以
,所以 ,所以M的方程为
,所以M的方程为 .
.
(Ⅱ)因为CD⊥AB,直线AB方程为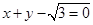 ,所以设直线CD方程为
,所以设直线CD方程为 ,
,
将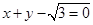 代入
代入 得:
得: ,即
,即 、
、 ,所以可得
,所以可得
 ;将
;将 代入
代入 得:
得: ,设
,设
 则
则
 =
= ,又因为
,又因为 ,即
,即 ,所以当
,所以当 时,|CD|取得最大值4,所以四边形ACBD面积的最大值为
时,|CD|取得最大值4,所以四边形ACBD面积的最大值为
 .
.
本题第(Ⅰ)问,属于中点弦问题,运用设而不求的数学思想;第(Ⅱ)问,运用弦长公式求出弦长,然后由面积公式求出面积的最大值.对第(Ⅰ)问,一部分同学想不到设而不求的思想,容易联立方程组求解而走弯路;第(Ⅱ)问,容易出现计算失误.
【考点定位】本小题考查椭圆的方程的求解、直线与椭圆的位置关系,考查数学中的待定系数法、设而不求思想 ,考查同学们的计算能力以及分析问题、解决问题的能力.圆锥曲线是高考的热点问题,年年必考,熟练本部分的基础知识是解答好本类问题的关键.

 则
则 ,
, ,(1)-(2)得:
,(1)-(2)得: ,因为
,因为 ,设
,设 ,因为P为AB的中点,且OP的斜率为
,因为P为AB的中点,且OP的斜率为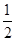 ,所以
,所以 ,即
,即 ,所以可以解得
,所以可以解得 ,即
,即 ,即
,即 ,又因为
,又因为 ,所以
,所以 ,所以M的方程为
,所以M的方程为 .
.(Ⅱ)因为CD⊥AB,直线AB方程为
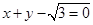 ,所以设直线CD方程为
,所以设直线CD方程为 ,
,将
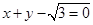 代入
代入 得:
得: ,即
,即 、
、 ,所以可得
,所以可得 ;将
;将 代入
代入 得:
得: ,设
,设
 则
则 =
= ,又因为
,又因为 ,即
,即 ,所以当
,所以当 时,|CD|取得最大值4,所以四边形ACBD面积的最大值为
时,|CD|取得最大值4,所以四边形ACBD面积的最大值为
 .
.本题第(Ⅰ)问,属于中点弦问题,运用设而不求的数学思想;第(Ⅱ)问,运用弦长公式求出弦长,然后由面积公式求出面积的最大值.对第(Ⅰ)问,一部分同学想不到设而不求的思想,容易联立方程组求解而走弯路;第(Ⅱ)问,容易出现计算失误.
【考点定位】本小题考查椭圆的方程的求解、直线与椭圆的位置关系,考查数学中的待定系数法、设而不求思想 ,考查同学们的计算能力以及分析问题、解决问题的能力.圆锥曲线是高考的热点问题,年年必考,熟练本部分的基础知识是解答好本类问题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
 在
在 轴右边,
轴右边,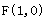 的距离减去它到
的距离减去它到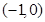 的直线
的直线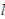 与曲线C有两个交点
与曲线C有两个交点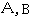 ,且
,且 ,求直线
,求直线 的斜率.
的斜率.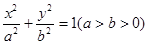 的离心率为
的离心率为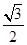 ,
,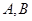 是其左右顶点,
是其左右顶点,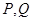 是椭圆上位于
是椭圆上位于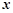 轴两侧的点(点
轴两侧的点(点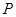 在
在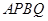 面积的最大值为4.
面积的最大值为4.
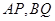 的斜率分别为
的斜率分别为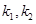 ,若
,若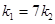 ,设△
,设△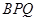 与△
与△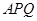 的面积分别为
的面积分别为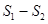 ,求
,求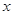 轴上,一个顶点为
轴上,一个顶点为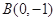 ,且其右焦点到直线
,且其右焦点到直线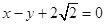 的距离为3.
的距离为3.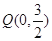 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点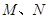 ,且满足
,且满足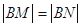 .
. 是椭圆
是椭圆 和双曲线
和双曲线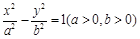 的公共顶
的公共顶 是双曲线上的动点,
是双曲线上的动点,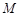 是椭圆上的动点(
是椭圆上的动点( 、
、 ),且满足
),且满足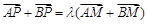 ,其中
,其中 ,设直线
,设直线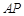 、
、 、
、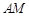 、
、 的斜率 分别记为
的斜率 分别记为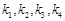 ,
,  ,则
,则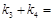
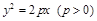 的焦点为
的焦点为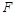 ,
,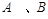 在抛物线上,且
在抛物线上,且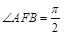 ,弦
,弦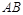 的中点
的中点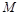 在其准线上的射影为
在其准线上的射影为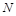 ,则
,则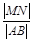 的最大值为________。
的最大值为________。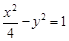 的顶点到渐进线的距离等于( )
的顶点到渐进线的距离等于( )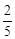

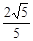
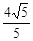
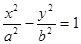 与
与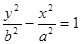 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为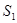 ,连接其四个焦点组成的四边形的面积为
,连接其四个焦点组成的四边形的面积为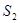 ,则
,则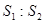 的最大值是
的最大值是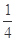
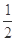
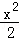 +y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .
+y2=1有公共的焦点,且它们的离心率互为倒数,则该双曲线的方程是 .