题目内容
如图,椭圆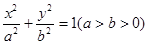 的离心率为
的离心率为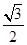 ,
,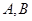 是其左右顶点,
是其左右顶点,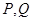 是椭圆上位于
是椭圆上位于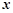 轴两侧的点(点
轴两侧的点(点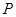 在
在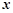 轴上方),且四边形
轴上方),且四边形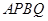 面积的最大值为4.
面积的最大值为4.

(1)求椭圆方程;
(2)设直线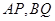 的斜率分别为
的斜率分别为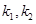 ,若
,若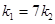 ,设△
,设△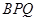 与△
与△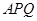 的面积分别为
的面积分别为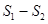 ,求
,求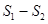 的最大值.
的最大值.
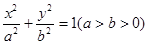 的离心率为
的离心率为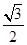 ,
,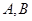 是其左右顶点,
是其左右顶点,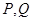 是椭圆上位于
是椭圆上位于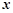 轴两侧的点(点
轴两侧的点(点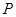 在
在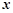 轴上方),且四边形
轴上方),且四边形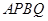 面积的最大值为4.
面积的最大值为4.
(1)求椭圆方程;
(2)设直线
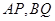 的斜率分别为
的斜率分别为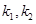 ,若
,若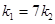 ,设△
,设△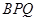 与△
与△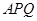 的面积分别为
的面积分别为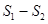 ,求
,求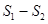 的最大值.
的最大值.(1) ; (2)
; (2) 的最大值为
的最大值为 .
.
 ; (2)
; (2) 的最大值为
的最大值为 .
. 试题分析:(1)由
 2分,得
2分,得 ,所以椭圆方程为
,所以椭圆方程为 ; 4分
; 4分(2)设
 ,设直线
,设直线 的方程为
的方程为 ,代入
,代入 得
得 , 5分
, 5分 ,
, , 7分
, 7分 ,
, ,由
,由 得
得 ,
,所以
 ,所以
,所以 , 8分
, 8分得
 ,得
,得 ,① 9分
,① 9分 ,
, , 10分
, 10分代入①得
 ,得
,得 ,或
,或 (是增根,舍去), 11分
(是增根,舍去), 11分所以
 12分
12分所以

 ,当
,当 时取到, 14分
时取到, 14分所以

 ,所以
,所以 的最大值为
的最大值为 . ` 15分
. ` 15分点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求椭圆标准方程时,主要运用了椭圆的几何性质,建立了a,bac的方程组。(2)作为研究三角形面积问题,应用韦达定理,建立了m的函数式,利用函数观点,求得面积之差的最大值,使问题得解。

练习册系列答案
相关题目
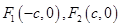 分别是椭圆
分别是椭圆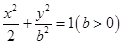 的左、右焦点,椭圆的离心率
的左、右焦点,椭圆的离心率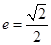 .
.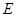 的方程;(II)已知直线
的方程;(II)已知直线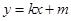 与椭圆
与椭圆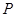 ,且与直线
,且与直线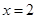 相交于点
相交于点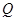 .求证:以线段
.求证:以线段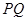 为直径的圆恒过定点
为直径的圆恒过定点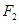 .
.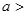
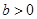 ,曲线
,曲线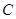 上任意一点
上任意一点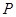 分别与点
分别与点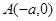 、
、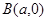 连线的斜率的乘积为
连线的斜率的乘积为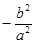 .
.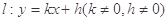 与
与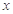 轴、
轴、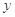 轴分别交于
轴分别交于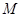 、
、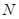 两点,若曲线
两点,若曲线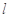 没有公共点,求证:
没有公共点,求证: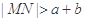 .
.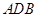 为半圆,
为半圆,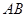 为半圆直径,
为半圆直径,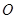 为半圆圆心,且
为半圆圆心,且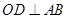 ,
,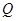 为线段
为线段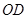 的中点,已知
的中点,已知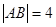 ,曲线
,曲线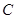 过
过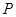 在曲线
在曲线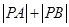 的值不变.
的值不变.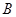 的直线
的直线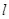 与曲线
与曲线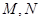 两点,与
两点,与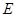 点,
点,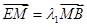 ,
,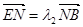 证明:
证明: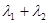 为定值.
为定值.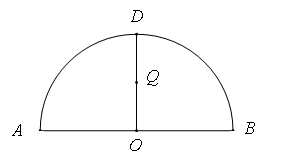
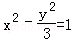 的渐近线的距离是( )
的渐近线的距离是( )
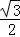
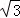
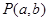 与点
与点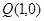 在直线
在直线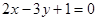 的两侧,则下列说法:
的两侧,则下列说法: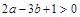 ;
;  时,
时,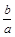 有最小值,无最大值;
有最小值,无最大值;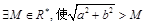 恒成立
恒成立 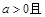
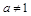 ,
,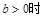 , 则
, 则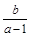 的取值范围为(-
的取值范围为(-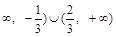
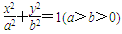 的离心率e为
的离心率e为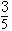 , 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
, 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.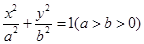 右焦点的直线
右焦点的直线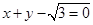 交
交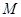 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为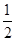 .
.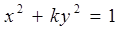 的离心率是2,则实数k的值是
的离心率是2,则实数k的值是