题目内容
已知椭圆的中心在原点,焦点在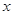 轴上,一个顶点为
轴上,一个顶点为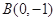 ,且其右焦点到直线
,且其右焦点到直线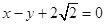 的距离为3.
的距离为3.
(Ⅰ)求椭圆方程;
(Ⅱ)设直线过定点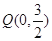 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点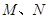 ,且满足
,且满足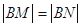 .
.
求直线的方程.
 轴上,一个顶点为
轴上,一个顶点为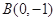 ,且其右焦点到直线
,且其右焦点到直线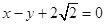 的距离为3.
的距离为3.(Ⅰ)求椭圆方程;
(Ⅱ)设直线过定点
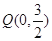 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点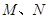 ,且满足
,且满足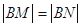 .
.求直线的方程.
(1)
(2)) 或
或 .
.

(2))
 或
或 .
.试题分析:(1)设椭圆方程为
 , 则
, 则 . 1分
. 1分 令右焦点
 , 则由条件得
, 则由条件得 ,得
,得 3分
3分 那么
 ,∴椭圆方程为
,∴椭圆方程为 . 4分
. 4分 (2)若直线斜率不存在时,直线即为
 轴,此时
轴,此时 为椭圆的上下顶点,
为椭圆的上下顶点, ,不满足条件; 5分
,不满足条件; 5分故可设直线:
 ,与椭圆
,与椭圆 联立,
联立,消去
 得:
得:  . 6分
. 6分由
 ,得
,得 . 7分
. 7分 由韦达定理得

而
 8分
8分 设
 的中点
的中点 ,则
,则
由
 ,则有
,则有 .
. 10分
10分可求得
 . 11分
. 11分 检验
 12分
12分 所以直线方程为
 或
或 . 3分
. 3分 点评:主要是考查了直线与椭圆的位置关系的运用,属于基础题。

练习册系列答案
相关题目
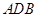 为半圆,
为半圆,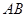 为半圆直径,
为半圆直径, 为半圆圆心,且
为半圆圆心,且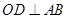 ,
,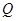 为线段
为线段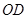 的中点,已知
的中点,已知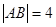 ,曲线
,曲线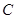 过
过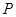 在曲线
在曲线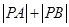 的值不变.
的值不变.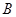 的直线
的直线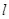 与曲线
与曲线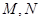 两点,与
两点,与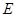 点,
点,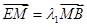 ,
,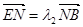 证明:
证明: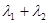 为定值.
为定值.
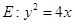 的焦点为F,准线
的焦点为F,准线 与x轴的交点为A.点C在抛物线E上,以C为圆心,
与x轴的交点为A.点C在抛物线E上,以C为圆心,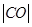 为半径作圆,设圆C与准线
为半径作圆,设圆C与准线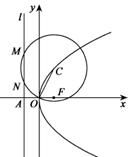
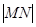 ;
;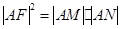 ,求圆C的半径.
,求圆C的半径.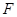 是抛物线
是抛物线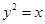 的焦点,
的焦点,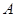 、
、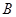 是该抛物线上的两点,且
是该抛物线上的两点,且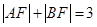 ,则线段
,则线段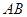 的中点到
的中点到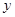 轴的距离为( )
轴的距离为( )
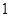
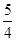
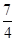
 与点
与点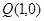 在直线
在直线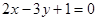 的两侧,则下列说法:
的两侧,则下列说法: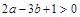 ;
;  时,
时,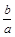 有最小值,无最大值;
有最小值,无最大值;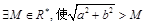 恒成立
恒成立 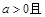
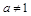 ,
,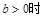 , 则
, 则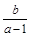 的取值范围为(-
的取值范围为(-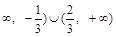
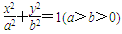 的离心率e为
的离心率e为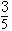 , 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
, 且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.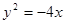
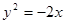
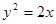
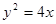
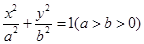 右焦点的直线
右焦点的直线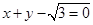 交
交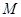 于A,B两点,P为AB的中点,且OP的斜率为
于A,B两点,P为AB的中点,且OP的斜率为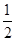 .
.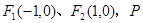 是椭圆上一点且
是椭圆上一点且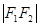 是
是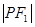 与
与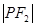 的等差中项,则此椭圆的标准方程为 。
的等差中项,则此椭圆的标准方程为 。