题目内容
已知数列{an}中，a1=1,an+1=
(an+
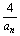)(n∈N*),且{an}存在极限。
（1）证明：{an}时先增后减数列，并求an的最大值；
（2）已知圆锥曲线Cn的方程为：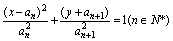
设
Cn=C,求曲线C的方程并求曲线C的面积。
得an=an-1=…=an=a1=2，这与条件矛盾，因此，an≠2对n∈
N*恒成立. ∴当n≥2时，an>2.
又n≥2时，
an-an+1=an-
∴a1,<a2,a2<a3>…an>an+1>…>2,即{an}是行列增后减数列，（an）max=a2=
练习册系列答案
相关题目
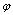)(x∈R)(其中A>O,w>0)的图像在y轴右侧的第一个最高点为M(2，2
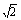)，与x轴在原点右侧的第一个交点为N(0,0) 
（
）=1，则常数a,b的值为 （ ）
-2,b=4 B．a=2,b=-4
与直线
，直线
分别交于
两点，
中点为
，则直线
B、
C、
D、
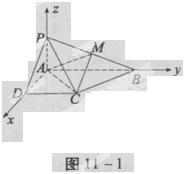
AB=1，M是PB的中点。