题目内容
已知sinαcosα＜0,sinαtanα＜0.化简
.
解析：∵sinαcosα＜0,∴α是二、四象限角.
又∵sinαtanα＜0,∴α是二、三象限角.由此得α为第二象象限角，α2为一、三象限角.
当α2在第一象限时，
原式=.
当
在第三象限时,
原式=-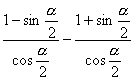
=-
.
练习册系列答案
相关题目
题目内容
已知sinαcosα＜0,sinαtanα＜0.化简.
解析：∵sinαcosα＜0,∴α是二、四象限角.
又∵sinαtanα＜0,∴α是二、三象限角.由此得α为第二象象限角，α2为一、三象限角.
当α2在第一象限时，
原式=.
当在第三象限时,
原式=-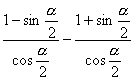=-.