题目内容
已知函数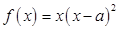 ,
,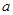 是大于零的常数.
是大于零的常数.
(Ⅰ)当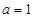 时,求
时,求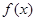 的极值;
的极值;
(Ⅱ)若函数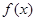 在区间
在区间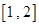 上为单调递增,求实数
上为单调递增,求实数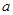 的取值范围;
的取值范围;
(Ⅲ)证明:曲线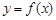 上存在一点
上存在一点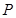 ,使得曲线
,使得曲线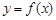 上总有两点
上总有两点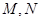 ,且
,且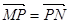 成立.
成立.
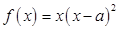 ,
,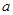 是大于零的常数.
是大于零的常数. (Ⅰ)当
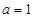 时,求
时,求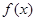 的极值;
的极值;(Ⅱ)若函数
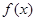 在区间
在区间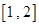 上为单调递增,求实数
上为单调递增,求实数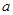 的取值范围;
的取值范围;(Ⅲ)证明:曲线
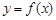 上存在一点
上存在一点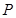 ,使得曲线
,使得曲线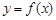 上总有两点
上总有两点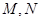 ,且
,且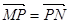 成立.
成立.(I)极大值 ,极小值
,极小值 .
.
(Ⅱ)当函数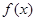 在区间
在区间 上为单调递增时,
上为单调递增时, 或
或 .
.
(Ⅲ)曲线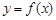 上存在一点
上存在一点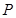
 ,使得曲线
,使得曲线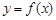 上总有两点
上总有两点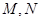 ,且
,且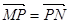 成立 .
成立 .
 ,极小值
,极小值 .
.(Ⅱ)当函数
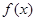 在区间
在区间 上为单调递增时,
上为单调递增时, 或
或 .
. (Ⅲ)曲线
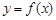 上存在一点
上存在一点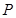
 ,使得曲线
,使得曲线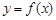 上总有两点
上总有两点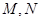 ,且
,且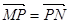 成立 .
成立 .试题分析:(I)求极值一般遵循“求导数、求驻点、讨论区间的导数值正负、计算极值”.
(Ⅱ)函数
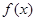 在区间
在区间 上为单调递增,因此,其导函数为正数恒成立,据此建立
上为单调递增,因此,其导函数为正数恒成立,据此建立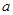 的不等式求解.
的不等式求解.应注意结合
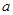 的不同取值情况加以讨论.
的不同取值情况加以讨论.(Ⅲ)通过确定函数的极大值、极小值点
 ,
, , 并确定
, 并确定 的中点
的中点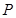
 .
. 设
 是图象任意一点,由
是图象任意一点,由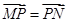 ,可得
,可得 ,
,根据

 ,可知点
,可知点 在曲线
在曲线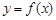 上,作出结论.
上,作出结论.本题难度较大,关键是能否认识到极大值、极小值点
 ,
, 的中点即为所求.
的中点即为所求.试题解析:(I)
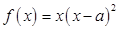 ,
,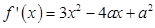 ,
,当
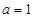 时,
时, ,
,令
 得
得 .
.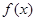 在
在 分别单调递增、单调递减、单调递增,
分别单调递增、单调递减、单调递增,于是,当
 时,函数有极大值
时,函数有极大值 ,
, 时,有极小值
时,有极小值 .
.------4分
(Ⅱ)
 ,若函数
,若函数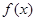 在区间
在区间 上为单调递增,
上为单调递增,则
 在
在 上恒成立,
上恒成立,当
 ,即
,即 时,由
时,由 得
得 ;
;当
 ,即
,即 时,
时, ,无解;
,无解;当
 ,即
,即 时,由
时,由 得
得 .
.综上,当函数
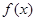 在区间
在区间 上为单调递增时,
上为单调递增时, 或
或 . 10分
. 10分(Ⅲ)
 ,
, ,
,令
 ,得
,得 ,
, 在区间
在区间 ,
, ,
, 上分别单调递增,单调递减,单调递增,
上分别单调递增,单调递减,单调递增,于是当
 时,有极大值
时,有极大值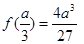 ;
;当
 时,有极小值
时,有极小值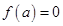 .
.记
 ,
, ,
,  的中点
的中点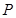
 ,
, 设
 是图象任意一点,由
是图象任意一点,由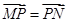 ,得
,得 ,
,因为

 ,
,由此可知点
 在曲线
在曲线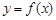 上,即满足
上,即满足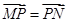 的点
的点 在曲线
在曲线 上.
上.所以曲线
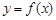 上存在一点
上存在一点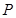
 ,使得曲线
,使得曲线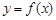 上总有两点
上总有两点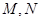 ,且
,且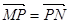 成立 . 14分
成立 . 14分
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
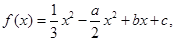 其中
其中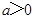 ,曲线
,曲线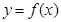 在点
在点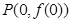 处的切线方程为
处的切线方程为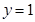 .
.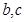 的值;
的值;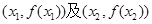 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当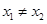 时,
时,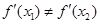 ;
;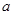 的取值范围.
的取值范围.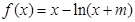
 的单调区间和极值;
的单调区间和极值; 恒成立?
恒成立? 时,方程
时,方程 内有唯一实根.
内有唯一实根. .)
.)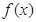 =
=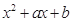 ,
,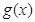 =
=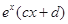 ,若曲线
,若曲线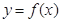 和曲线
和曲线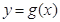 都过点P(0,2),且在点P处有相同的切线
都过点P(0,2),且在点P处有相同的切线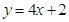 .
.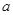 ,
,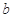 ,
,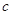 ,
,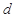 的值;
的值;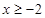 时,
时,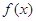 ≤
≤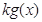 ,求
,求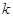 的取值范围.
的取值范围. ,
, .
. ;
; 与
与 、
、 均相切,切点分别为(
均相切,切点分别为( )、(
)、( ),且
),且 ,求证:
,求证: .
. ,
, 的单调性;
的单调性; .
. 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,则函数
,则函数 的图象在点
的图象在点 处的切线方程为 .
处的切线方程为 . ,若
,若 在
在 上的极值点分别为
上的极值点分别为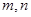 ,则
,则 的值为( )
的值为( )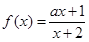 在
在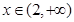 上单调递减,则实数
上单调递减,则实数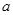 的取值范围是 .
的取值范围是 .