题目内容
【题目】已知椭圆C： 
+y2=1． （Ⅰ）求椭圆C的长轴和短轴的长，离心率e，左焦点F1；
（Ⅱ）经过椭圆C的左焦点F1作直线l，直线l与椭圆C相交于A，B两点，若|AB|= 
，求直线l的方程．
【答案】解：（Ⅰ）由椭圆 
，可知a2=2，b2=1，则 
，故c=1 ∴椭圆C的长轴 
，短轴2b=2，离心率 
，
左焦点F1（﹣1，0）．）
（Ⅱ）设直线l方程y=k（x+1），联立方程组：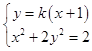 
，消元得：（2k2+1）x2+4k2x+2k2﹣2=0，
设A（x1 ， y1），B（x2 ， y2）
则由韦达定理可知： 
， 
，
则弦长公式： 
，
∴ 
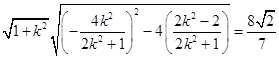
即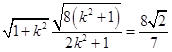 
解得：k2=3， 
，
∴直线l的方程： 
或 
即 
或 
【解析】（Ⅰ）由椭圆的方程可知： 
，故c=1，椭圆C的长轴 
，短轴2b=2，离心率 
，左焦点F1（﹣1，0）；（Ⅱ）设直线l方程y=k（x+1），代入椭圆方程，由韦达定理及弦长公式即可求得k的值，即可求得直线l的方程．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
