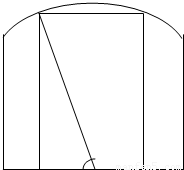
题目内容
如图，钢板材料ABCD，上沿为圆弧AD，其所在圆的圆心为BC中点O，AB、CD都垂直于BC，且AB=CD=| 3 |
（1）求矩形EFGH的面积S关于θ的函数表达式S=f（θ）；
（2）求矩形面积S的最大值．
分析：（1）矩形EFGH的面积S=EF×EH，关键是利用已知角表达出EF，EH；
（2）由（1）得S=4sin2θ，从而可求面积的最大值．
（2）由（1）得S=4sin2θ，从而可求面积的最大值．
解答：解：（1）在Rt△ABO中，由AB=
，BO=1得：r=AO=2
在Rt△HEO中，由OH=r=2，∠BOH=θ，得：HE=2sinθ，EO=2cosθ，
∴S=f（θ）=EF×EH=8 sinθ×cosθ=4sin2θ．
（2）由（1）得S=4sin2θ，∴θ=45°时，Smax=4米2．
| 3 |
在Rt△HEO中，由OH=r=2，∠BOH=θ，得：HE=2sinθ，EO=2cosθ，
∴S=f（θ）=EF×EH=8 sinθ×cosθ=4sin2θ．
（2）由（1）得S=4sin2θ，∴θ=45°时，Smax=4米2．
点评：本题借助于引进角，将面积用角参数表示，从而求面积的最大值．
练习册系列答案
阅读快车系列答案
相关题目
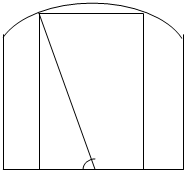
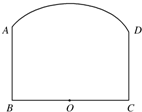如图，钢板材料ABCD的上沿为圆弧AD，其所在圆的圆心为BC的中点O，AB、CD都垂直于BC，且AB=CD=a，BC=b，现如何用这块钢板材料截一块矩形板（其中两个顶点在
（2012•江苏一模）现有一张长为80cm，宽为60cm的长方形铁皮ABCD，准备用它做成一只无盖长方体铁皮盒，要求材料利用率为100%，不考虑焊接处损失．如图，若长方形ABCD的一个角剪下一块铁皮，作为铁皮盒的底面，用余下材料剪拼后作为铁皮盒的侧面，设长方体的底面边长为x （cm），高为y （cm），体积为V （cm3）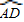
上，另两个顶点在BC上），使矩形的面积最大？请你设计截取方案，并说明理由．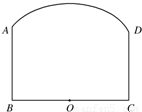
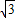米，BC=2米，现要用这块钢板材料截成一块矩形板EFGH（其中G，H在AD上，E，F在BC上），设∠BOH=θ．