题目内容
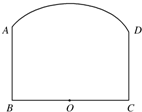 如图,钢板材料ABCD的上沿为圆弧AD,其所在圆的圆心为BC的中点O,AB、CD都垂直于BC,且AB=CD=a,BC=b,现如何用这块钢板材料截一块矩形板(其中两个顶点在
如图,钢板材料ABCD的上沿为圆弧AD,其所在圆的圆心为BC的中点O,AB、CD都垂直于BC,且AB=CD=a,BC=b,现如何用这块钢板材料截一块矩形板(其中两个顶点在 | AD |
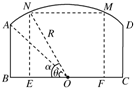
分析:作出如图的辅助线,设∠AOB=θ,∠NOB=α,化简矩形EFMN的面积得S=R2sin 2α,由于2θ≤2α<π,所以分θ≤
与θ>
两种情况讨论,分别根据sin2α的最大值得到矩形面积S的最大值,由此即可得到相应的设计方案.
| π |
| 4 |
| π |
| 4 |
解答:解:如图,设∠AOB=θ,∠NOB=α(θ≤α≤
),
其中半径AO=R=
,且sin θ=
,cos θ=
.
矩形EFMN的面积是
S=Rsinα(2Rcosα)=R2sin2α(2θ≤2α<π),
①当θ≤
,即2θ≤
时,此时2a≤b,Smax=R2=a2+
b2,这时α=
.
②当θ>
,即2θ>
时,此时2a>b,Smax=R2sin 2θ=2R2sin θcos θ=2R2•
•
=ab.
因此,设计方案如下:
当2a≤b时,取点N使∠NOB=
,再确定点M、E、F,这样矩形EFMN的最大面积为a2+
b2;
当2a>b时,这时矩形ABCD就是所求的面积最大的矩形,最大面积为ab.
| π |
| 2 |

其中半径AO=R=
a2+
|
| a |
| R |
| b |
| 2R |
矩形EFMN的面积是
S=Rsinα(2Rcosα)=R2sin2α(2θ≤2α<π),
①当θ≤
| π |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
| π |
| 4 |
②当θ>
| π |
| 4 |
| π |
| 2 |
| a |
| R |
| b |
| 2R |
因此,设计方案如下:
当2a≤b时,取点N使∠NOB=
| π |
| 4 |
| 1 |
| 4 |
当2a>b时,这时矩形ABCD就是所求的面积最大的矩形,最大面积为ab.
点评:本题在圆当中求截取矩形的面积最大值,着重考查了解三角形、三角函数的值域与最值和三角函数的应用等知识,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3)
(2012•江苏一模)现有一张长为80cm,宽为60cm的长方形铁皮ABCD,准备用它做成一只无盖长方体铁皮盒,要求材料利用率为100%,不考虑焊接处损失.如图,若长方形ABCD的一个角剪下一块铁皮,作为铁皮盒的底面,用余下材料剪拼后作为铁皮盒的侧面,设长方体的底面边长为x (cm),高为y (cm),体积为V (cm3) 如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD=
如图,钢板材料ABCD,上沿为圆弧AD,其所在圆的圆心为BC中点O,AB、CD都垂直于BC,且AB=CD=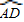 上,另两个顶点在BC上),使矩形的面积最大?请你设计截取方案,并说明理由.
上,另两个顶点在BC上),使矩形的面积最大?请你设计截取方案,并说明理由.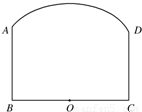
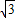 米,BC=2米,现要用这块钢板材料截成一块矩形板EFGH(其中G,H在AD上,E,F在BC上),设∠BOH=θ.
米,BC=2米,现要用这块钢板材料截成一块矩形板EFGH(其中G,H在AD上,E,F在BC上),设∠BOH=θ.