题目内容
设数列{an}的各项均为正数，它的前n项和为Sn(n∈N*)，已知点(an，4Sn)在函数f(x)=x2+2x+1的图象上， (1)证明{an}是等差数列，并求an；
(2)设m、k、p∈N*，m+p=2k，求证：
；
(3)对于(2)中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．
(2)设m、k、p∈N*，m+p=2k，求证：
；(3)对于(2)中的命题，对一般的各项均为正数的等差数列还成立吗？如果成立，请证明你的结论，如果不成立，请说明理由．
解：(1)∵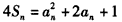
，
∴
，
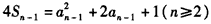两式相减得，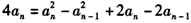
，
整理得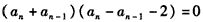
，
∵
，
∴
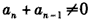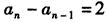(常数)，
∴{an}是以2为公差的等差数列．
又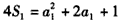
，即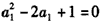
，
解得a1=1，
∴
。
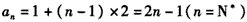(2)由(1)知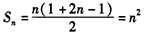
，
∴
，
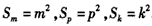由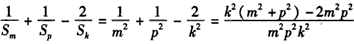
，
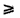
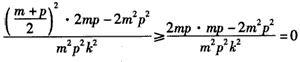即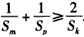
。
(3)结论成立，
证明如下：设等差数列{an}的首项为a1，公差为d，
则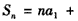
，
∵
，
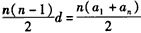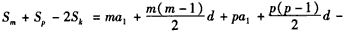
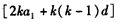
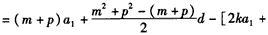
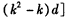把m+p=2k代入上式化简得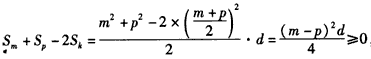
，
∴
，
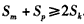又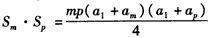
∴
，
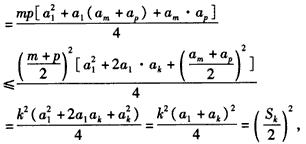
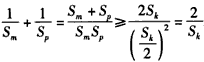故原不等式得证．
，∴
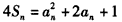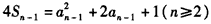，两式相减得，
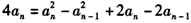，整理得
，∵
，∴
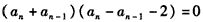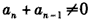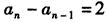(常数)， ∴{an}是以2为公差的等差数列．
又
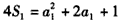，即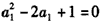，解得a1=1，
∴
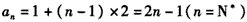。 (2)由(1)知
，∴
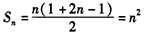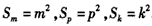，由
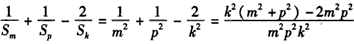
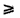
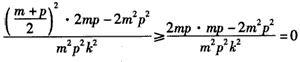，即
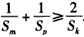。(3)结论成立，
证明如下：设等差数列{an}的首项为a1，公差为d，
则
，∵
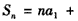
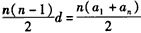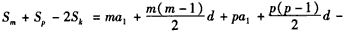
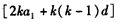
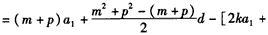
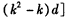，把m+p=2k代入上式化简得
，∴
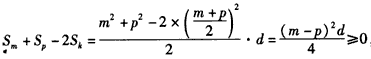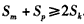，又
∴
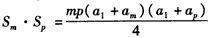
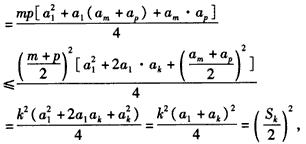
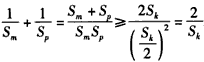，故原不等式得证．
练习册系列答案
相关题目