题目内容
设F是双曲线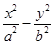
＝1的右焦点，双曲线两条渐近线分别为l1，l2，过F作直线l1的垂线，分别交l1，l2于A、B两点．若OA，AB，OB成等差数列，且向量
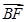与
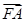同向，则双曲线离心率e的大小为________．
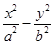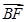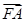＝1的右焦点，双曲线两条渐近线分别为l1，l2，过F作直线l1的垂线，分别交l1，l2于A、B两点．若OA，AB，OB成等差数列，且向量与同向，则双曲线离心率e的大小为________．
设OA＝m－d，AB＝m，OB＝m＋d，由勾股定理，得(m－d)2＋m2＝(m＋d)2.解得m＝4d.设∠AOF＝α，则cos 2α＝
＝
.cos α＝
＝
，所以，离心率e＝
＝.
＝.cos α＝＝，所以，离心率e＝＝.
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
，一个焦点到最近顶点的距离是
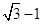，则双曲线的方程是（ ）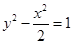
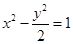
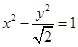
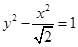
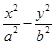＝1(a＞0，b＞0)的左、右焦点分别为F1，F2，点O为双曲线的中心，点P在双曲线右支上，△PF1F2内切圆的圆心为Q，圆Q与x轴相切于点A，过F2作直线PQ的垂线，垂足为B，则下列结论成立的是( )
到双曲线
的渐近线的距离为______________.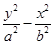
＝1(a>0，b>0)，P为x轴上一动点，经过P的直线y＝2x＋m(m≠0)与双曲线C有且只有一个交点，则双曲线C的离心率为________．
－
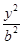＝1(a>0，b>0)的两个焦点，P是C上一点，若|PF1|＋|PF2|＝6a且△PF1F2的最小内角为30°，则双曲线C的离心率为________．
，虚轴长为4， 则该双曲线的标准方程是 
＝1(a>0，b>0)的实轴长为2，焦距为4，则该双曲线的渐近线方程是( )．
x
x