Question

已知

1

m

+

1

n

=1（m＞0，n＞0），当mn取得最小值时，直线y=-

2

x+2与曲线

x|x|

m

+

y|y|

n

=1的交点个数为

2

．

Answer 1

分析：由基本不等式可求mn取得最小值时的m，n的值，然后讨论：当x＞0，y＞0；②当x＞0，y＜0，③当x＜0，y＞0；④当x＜0，y＜0四种情况分别求出方程所表示的曲线，作出图象能得到结果

解答：解：由基本不等式可得，1=

1

m

+

1

n

≥2

1 mn

∴mn≥4
当且仅当

1

m

=

1

n

=

1

2

时等号成立，
也就是所以m=2，n=2．
∵曲线

x|x|

m

+

y|y|

n

=1
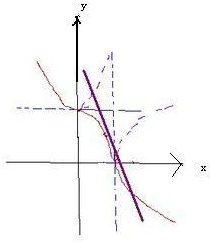
∴①当x＞0，y＞0，x²+y²=2表示 圆心在原点，半径为

2

的圆
②当x＞0，y＜0，x²-y²=2 以x轴为实轴的双曲线；
③当x＜0，y＞0，y²-x²=2表示以y轴为实轴的双曲线；
④当x＜0，y＜0，x²+y²=-2此时无解．
所以如图得到图象，
结合图象知直线y=-

2

x+2与曲线交点个数是2个．
故答案为：2．

点评：本题考查直线与圆锥曲线的综合应用，解题时要注意均值定理和分类讨论思想、数形结合思想的合理运用．对数学思维的要求比较高，有一定的探索性．综合性强，难度大，常因分类不清易出错，是高考的重点．