题目内容
已知直线y-1=k(x-1)恒过定点A,若点A在直线mx+ny-1=0(m,n>0)上,则
+
的最小值为( )
| 1 |
| m |
| 1 |
| n |
分析:由直线系方程求出直线经过的定点,把定点坐标代入直线mx+ny-1=0,得到m+n=1,把
+
乘以“1”,即乘以m+n,
展开后运用基本不等式求其最小值.
| 1 |
| m |
| 1 |
| n |
展开后运用基本不等式求其最小值.
解答:解:由
,得:
.
所以,直线y-1=k(x-1)恒过定点A(1,1).
又点A在直线mx+ny-1=0(m,n>0)上,
所以,m+n=1.
则
+
=(
+
)(m+n)=2+
+
.
因为m,n>0,
所以,
+
=2+
+
≥2+2
=4.
当且仅当m=n=
时等号成立.
故选C.
|
|
所以,直线y-1=k(x-1)恒过定点A(1,1).
又点A在直线mx+ny-1=0(m,n>0)上,
所以,m+n=1.
则
| 1 |
| m |
| 1 |
| n |
| 1 |
| m |
| 1 |
| n |
| n |
| m |
| m |
| n |
因为m,n>0,
所以,
| 1 |
| m |
| 1 |
| n |
| n |
| m |
| m |
| n |
|
当且仅当m=n=
| 1 |
| 2 |
故选C.
点评:本题考查直线系方程,考查了利用基本不等式求最值,涉及到定值为“1”的问题,灵活注意“1”的代换,此题是基础题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的最小值为
的最小值为

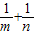 的最小值为( )
的最小值为( )

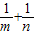 的最小值为( )
的最小值为( )
