题目内容
如图,已知DA⊥平面ABE,四边形ABCD是边长为2的正方形,在△ABE中,AE=1,BE=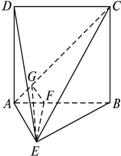
(1)证明平面ADE⊥平面BCE;
(2)求二面角B-AC-E的大小.
解法一:(1)证明:∵DA⊥平面ABE,∴DA⊥BE.

又在△ABE中,易知BE⊥EA,EA∩DA=A,
∴BE⊥平面ADE.
∵BE![]() 平面BCE,
平面BCE,
∴平面BCE⊥平面ADE.
(2)过点E作EF⊥AB于F,
∵DA⊥平面ABE,
∴平面ABCD⊥平面ABE.
∴EF⊥平面AC.作FG⊥AC于G,连结EG,则EG⊥AC,∠EGF就是二面角B-AC-E的平面角.
在Rt△EFG中,tan∠EGF=![]() =
=![]() =
=![]() ,
,
∴所求二面角的大小是arctan![]() .
.
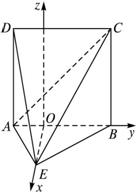
解法二:建立图示空间直角坐标系,则A(0,-![]() ,0),B(0,
,0),B(0,![]() ,0),C(0,
,0),C(0,![]() ,2),D(0,-
,2),D(0,-![]() ,2),E(
,2),E(![]() ,0,0),∴
,0,0),∴![]() =(0,2,2),
=(0,2,2),![]() =(0,0,2),
=(0,0,2),![]() =(
=(![]() ,
,![]() ,0),
,0), ![]() =(
=(![]() ,-
,-![]() ,0).
,0).
(1)∵![]() ·
·![]() =0,
=0, ![]() ·
·![]() =0,
=0,
∴AE⊥BC,AE⊥BE.
又BC∩BE=B,∴AE⊥平面BCE.
∵AE![]() 平面ADE,
平面ADE,
∴平面ADE⊥平面BCE.
(2)设n=(x,y,1)⊥平面ACE,由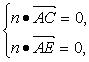 得n=(
得n=(![]() ,-1,1),又
,-1,1),又![]() 是平面ABCD的法向量,
是平面ABCD的法向量,
∵cos〈n, ![]() 〉=
〉=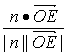 =
=![]() ,
,
∴所求二面角的大小是arccos![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
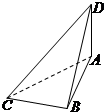 如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=
如图,已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=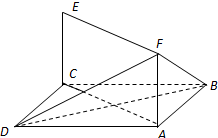 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,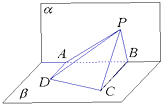 如图,已知平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,AD=4,BC=8,AB=6,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB的面积的最大值是( )
如图,已知平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,AD=4,BC=8,AB=6,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB的面积的最大值是( )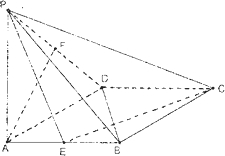 如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点. 如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.
如图,已知四面体ABCD的四个面均为锐角三角形,EFGH分别是边AB,BC,CD,DA上的点,BD||平面EFGH,且EH=FG.