题目内容
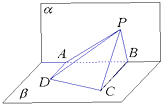 如图,已知平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,AD=4,BC=8,AB=6,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB的面积的最大值是( )
如图,已知平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,AD=4,BC=8,AB=6,在平面α上有一个动点P,使得∠APD=∠BPC,则△PAB的面积的最大值是( )分析:利用线面垂直的性质可以得到△PAD与△PBC是直角三角形,再由∠APD=∠BPC得到两直角三角形相似,
过P作PM⊥AB与M,则M为三角形PAB底边AB上的高,设出AM的长度t,通过解直角三角形把AM用含有t的代数式表示,代入三角形面积公式后利用配方法求面积的最大值.
过P作PM⊥AB与M,则M为三角形PAB底边AB上的高,设出AM的长度t,通过解直角三角形把AM用含有t的代数式表示,代入三角形面积公式后利用配方法求面积的最大值.
解答:解:由题意平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,
且DA⊥α,CB⊥α,∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,
∴△PAD∽△PBC,又AD=4,BC=8,
∴PB=2PA
如图,
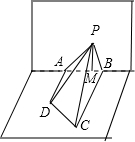
作PM⊥AB,垂足为M,令AM=t,
在两个Rt△PAM与Rt△PBM中,AM是公共边及PB=2PA
∴PA2-t2=4PA2-(6-t)2
解得PA2=12-4t
∴PM=
.
∴S=
×AB×PM=
×6×
=3
=3
≤12.
即三角形面积的最大值为12.
且DA⊥α,CB⊥α,∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,
∴△PAD∽△PBC,又AD=4,BC=8,
∴PB=2PA
如图,

作PM⊥AB,垂足为M,令AM=t,
在两个Rt△PAM与Rt△PBM中,AM是公共边及PB=2PA
∴PA2-t2=4PA2-(6-t)2
解得PA2=12-4t
∴PM=
| 12-4t-t2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 12-4t-t2 |
| 12-4t-t2 |
| 16-(t+2)2 |
即三角形面积的最大值为12.
点评:本题考查了平面与平面垂直的性质,考查了学生的空间想象能力,解答此题的关键是借助于三角形相似寻找关系,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
 如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
