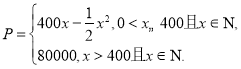题目内容
【题目】某同学在研究函数
时，给出下面几个结论中正确的有( )
A.
的图象关于点
对称B.若
，则
C.的值域为D.函数
有三个零点
【答案】BC
【解析】
先判断函数的奇偶性，再利用绝对值性质化简函数的解析式，判断函数的值域，然后再根据零点的定义判断即可.
函数
的定义域为全体实数，
，所以是奇函数，图象关于原点对称，
.
选项A：由上分析函数关于原点对称，若函数关于
对称，原点关于对称的点是
，而
，显然不在该图象上，故函数不关于对称，本选项是错误的；
选项B：当
时，
，显然函数单调递增，此时
；
当
时，
，显然函数单调递增，此时
，因此函数在整个实数集上是单调递增的，因此若
，则
是正确的，本选项是正确的；
选项C：由选项B的分析可以知道本选项是正确的；
选项D：
，只有一个零点，故本选项是错误的.
故选：BC
练习册系列答案
阅读快车系列答案
相关题目
