Question

已知函数f(x)＝ax＋bln x＋c(a，b，c是常数)在x＝e处的切线方程为(e－1)x＋ey－e＝0，且f(1)＝0.

(1)求常数a，b，c的值；

(2)若函数g(x)＝x²＋mf(x)(m∈R)在区间(1,3)内不是单调函数，求实数m的取值范围．

Answer 1

解：(1)由题设知，f(x)的定义域为(0，＋∞)，f′(x)＝a＋.

∵f(x)在x＝e处的切线方程为(e－1)x＋ey－e＝0，

∴f′(e)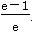＝－，且f(e)＝2－e，

即a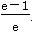＋＝－，且ae＋b＋c＝2－e.

又f(1)＝a＋c＝0，解得a＝－1，b＝1，c＝1.

(2)由(1)知f(x)＝－x＋ln x＋1(x>0)，

∴g(x)＝x²＋mf(x)＝x²－mx＋mln x＋m(x>0)，

∴g′(x)＝2x－m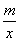＋＝(2x²－mx＋m)(x>0)．

令d(x)＝2x²－mx＋m(x>0)．

①当函数g(x)在(1,3)内有一个极值时，g′(x)＝0在(1,3)内有且仅有一个根，即d(x)＝2x²－mx＋m＝0在(1,3)内有且仅有一个根．

又∵d(1)＝2>0，∴当d(3)＝0，即m＝9时，d(x)＝2x²－mx＋m＝0在(1,3)内有且仅有一个根x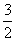＝；当d(3)≠0时，应有d(3)<0，即2×3²－3m＋m<0，解得m>9，∴m≥9.

②当函数g(x)在(1,3)内有两个极值时，g′(x)＝0在(1,3)内有两个根，即二次函数d(x)＝2x²－mx＋m＝0在(1,3)内有两个不等根，

所以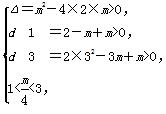

解得8<m<9.

综上，实数m的取值范围是(8，＋∞)．