题目内容
7．求tan（-690°）sin（-1050°）的值．分析 直接利用三角函数的诱导公式得答案．
解答 解：tan（-690°）sin（-1050°）=tan690°sin1050°
=tan（720°-30°）sin（1080°-30°）
=tan（-30°）sin（-30°）
=tan30°sin30°
=$\sqrt{3}×\frac{1}{2}=\frac{\sqrt{3}}{2}$．
点评 本题考查利用诱导公式化简求值，关键是对诱导公式的记忆，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
18．
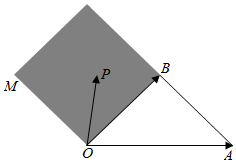如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（ ）
如图，OM∥AB，点P在由射线OM，线段OB及AB的延长线围成的阴影区域内（不含边界），且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，则实数对（x，y）可以是（ ）| A． | （$\frac{1}{4}$，$\frac{3}{4}$） | B． | （-$\frac{2}{3}$，$\frac{2}{3}$） | C． | （-$\frac{1}{4}$，$\frac{3}{4}$） | D． | （-$\frac{1}{5}$，$\frac{7}{5}$） |
15．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{4}$，$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$+λ$\overrightarrow{{e}_{2}}$（λ∈R），其中$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$为不共线的单位向量，若对符合上述条件的任意向量$\overrightarrow{a}$，$\overrightarrow{b}$恒有|$\overrightarrow{a}$-$\overrightarrow{b}$|≥$\frac{\sqrt{3}}{4}$，则$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$夹角的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5}{6}π$ |
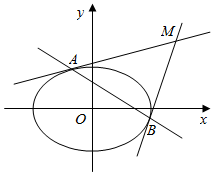教材器有介绍：圆x2+y2=r2上的点（x0，y0）处的切线方程为x0x+y0y=r2，我们将其结论推广：椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点（x0，y0）处的切线方程为$\frac{{x}_{0}x}{{a}^{2}}+\frac{{y}_{0}y}{{b}^{2}}$=1，在解本题时可以直接应用．已知，直线x-y+$\sqrt{3}$=0与椭圆E$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}$=1（a＞1）有且只有一个公共点
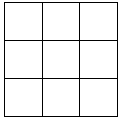将4个红球与2个蓝球（这些球只有颜色不同，其他完全相同）放入一个3×3的格子状木柜里（如图所示），每个格至多放一个球，则“所有红球均不位于相邻格子”的放法共有（ ）种．