题目内容
若直线l上的一个点P在平面α内，另一个点Q在平面α外，则直线l与平面α的位置关系是（ ）
| A、异面 | B、l?α |
| C、l∥α | D、l∩α=P |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：利用公理1进行推理
解答：
解：有题意可知，直线l经过平面α内一点A，和平面α外一点B，
直线l必定是α外的直线，
因为若l?α，则会出现点B∈α，与题设矛盾
∴l?α．
故选：D．
直线l必定是α外的直线，
因为若l?α，则会出现点B∈α，与题设矛盾
∴l?α．
故选：D．
点评：本题考查公理1的应用，反证法是解决本题的关键
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
C125+C126等于（ ）
| A、C135 |
| B、C136 |
| C、C1311 |
| D、A127 |
下列说法正确的是（ ）
| A、若命题p，?q都是真命题，则命题“p∧q”为真命题 |
| B、命题“若xy=0，则x=0或y=0”的否命题为“若xy≠0则x≠0或y≠0” |
| C、命题“?x∈R，2x＞0”的否定是“?x0∈R，2 x0≤0” |
| D、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
已知y=f（x）=ln|x|，则下列各命题中，正确的命题是（ ）
A、x＞0时，f′（x）=
| ||||
B、无论x＞0，还是x＜0，都有f′（x）=
| ||||
C、x＞0时，f′（x）=
| ||||
| D、因为x=0时，f（x）无意义，所以对于y=ln|x|不能求导 |
设Q是曲线T：xy=1（x＞0）上任意一点，l是曲线T在点Q处的切线，且l交坐标轴于A，B两点，则△OAB的面积（O为坐标原点）（ ）
| A、为定值2 |
| B、最小值为3 |
| C、最大值为4 |
| D、与点Q的位置有关 |
已知m，n，l为三条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（ ）
| A、α∥β，m?α，n?β⇒m∥n |
| B、l⊥β，α⊥β⇒l∥α |
| C、m⊥α，m⊥n，⇒n∥α |
| D、α∥β，l⊥α，n?β⇒l⊥n |
设i是虚数单位，则满足i2014•z=3-4i的复数z的共轭复数是（ ）
| A、-3-4i | B、-3+4i |
| C、3-4i | D、3+4i |
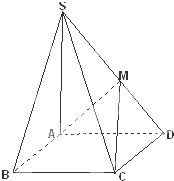如图，在四棱锥S-ABCD中，底面ABCD为矩形，SA⊥底面ABCD，M为SD的中点，且SA=AD=AB．