题目内容
已知直线 截圆心在点
截圆心在点 的圆
的圆 所得弦长为
所得弦长为 .
.
(1)求圆 的方程;
的方程;
(2)求过点 的圆
的圆 的切线方程.
的切线方程.
(1)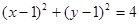
(2)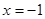 与
与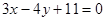
解析试题分析:(1)易知,圆心到直线的距离为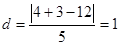 ,所以
,所以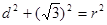 ,
,
所以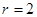 ,所以圆的方程为
,所以圆的方程为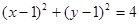 .
.
(2)当斜率不存在时,易知直线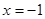 满足条件,当斜率存在时,设直线方程为
满足条件,当斜率存在时,设直线方程为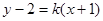 ,代入圆的方程得,
,代入圆的方程得,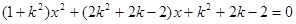 ,令
,令 得
得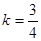 ,求得直线方程为
,求得直线方程为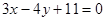 .故直线方程为
.故直线方程为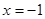 与
与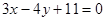 .
.
考点:直线与圆相交的性质;直线与圆的位置关系.
点评:本题主要考查利用待定系数法求圆的方程,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
相关题目
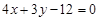 截圆心在点
截圆心在点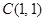 的圆
的圆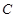 所得弦长为
所得弦长为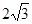 .
.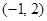 的圆
的圆 截圆心在点
截圆心在点 的圆
的圆 所得弦长为
所得弦长为 .
. 的圆
的圆