题目内容
(本小题满分6分)
已知直线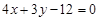 截圆心在点
截圆心在点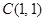 的圆
的圆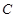 所得弦长为
所得弦长为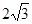 .
.
(1)求圆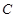 的方程;
的方程;
(2)求过点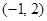 的圆
的圆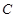 的切线方程.
的切线方程.
【答案】
(1)
(2) 与
与
【解析】
试题分析:(1)设圆C的半径为R , 圆心到直线 的距离为d .
的距离为d .
 ,
,
故圆C的方程为: ………………3分
………………3分
(2)当所求切线斜率不存在时,即 满足圆心到直线的距离为2,
满足圆心到直线的距离为2,
故 为所求的圆C的切线.…………………4分
为所求的圆C的切线.…………………4分
当切线的斜率存在时,可设方程为:  即
即
 解得
解得 故切线为:
故切线为:
整理得:
所以所求圆的切线为: 与
与 ……………6分
……………6分
考点:本题考查了圆的方程及直线与圆的位置关系
点评:在直线与圆的位置关系中,直线与圆相切时求切线、相交时求弦长是两个重点内容,要注意选择合适的方法去求解

练习册系列答案
相关题目
 上,并且与直线
上,并且与直线 相切于点
相切于点 的圆的方程.
的圆的方程. 的菱形
的菱形 中,
中, ,
, 面
面 ,
, 、
、 分别是
分别是 和
和 的中点.
的中点.
 面
面 ;
;  ⊥平面
⊥平面 ;
; 与平面
与平面
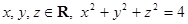 ,试求
,试求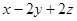 的最小值及相应
的最小值及相应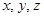 的值 。
的值 。